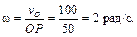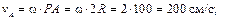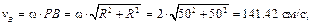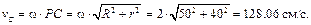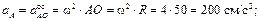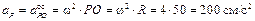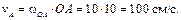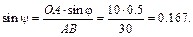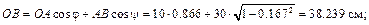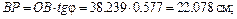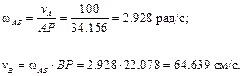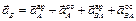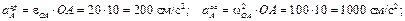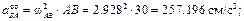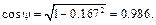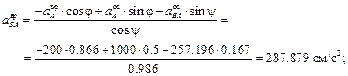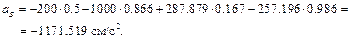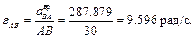Мцс 1 это что
Мгновенный центр скоростей
Мгнове́нный центр скоросте́й — при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело.
Содержание
Положение мгновенного центра скоростей
Для того, чтобы определить положение мгновенного центра скоростей, необходимо знать направления скоростей любых двух различных точек тела, скорости которых не параллельны. Тогда для определения положения мгновенного центра скоростей необходимо провести перпендикуляры к прямым, параллельным линейным скоростям выбранных точек тела. В точке пересечения этих перпендикуляров и будет находиться мгновенный центр скоростей.
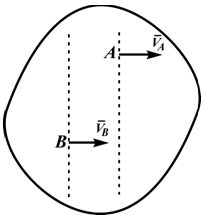
В том случае, если векторы линейных скоростей [1] двух различных точек тела параллельны друг другу, и отрезок, соединяющий эти точки, не перпендикулярен векторам этих скоростей, то перпендикуляры к этим векторам также параллельны. В этом случае говорят, что мгновенный центр скоростей находится в бесконечности, и тело движется мгновенно поступательно.
Если известны скорости двух точек, и эти скорости параллельны друг другу, и кроме того, указанные точки лежат на прямой, перпендикулярной скоростям, то положение мгновенного центра скоростей определяется так, как показано на рис. 2.
Положение мгновенного центра скоростей в общем случае не совпадает с положением мгновенного центра ускорений. Однако в некоторых случаях, например, при чисто вращательном движении, положения этих двух точек могут совпадать.
Более общий случай сферического движения
Согласно теореме вращения Эйлера, любое вращающееся трёхмерное тело, имеющее неподвижную точку, также имеет и ось вращения. Таким образом, в более общем случае вращения трёхмерного тела говорят о мгновенной оси вращения.
Пример решения задачи
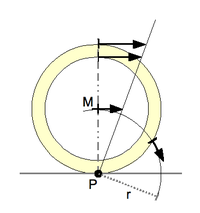
Найдём скорость точки K для колеса, показанного на рисунке 1, если задана скорость центра колеса (точки С), его радиус и угол АСК:
Найдём сначала угловую скорость колеса в данный момент времени при его вращении вокруг мгновенного центра скоростей (вокруг точки А):
Теперь, зная угловую скорость, найдём скорость точки К:
Чтобы найти численное значение 
, надо знать расстояние КА. Найдём его с помощью теоремы косинусов:
или, учтя, что 
, получим
Вынесем R за знак корня:
Подставив заданые в условии численные значения, найдём:
Тогда, зная расстояние КА, можем найти численное значение скорости по формуле (*):
Ответ: 
Заметим, что для решения задачи знать численное значение R не обязательно.
Действительно, подставляя в формулу (*) выражения для 
и для КА, получим
Применение понятия мгновенного центра скоростей
Движения коленного, локтевого, плечевого и др. суставов биофизики также исследуют с помощью мгновенного центра скоростей.
Улучшения тормозных характеристик автомобилей можно добиться путём выбора оптимальной конструкции педалей тормоза и соответствующих кинематических расчётов, проведённых с помощью мгновенного центра скоростей.
Примечания
Литература
Полезное
Смотреть что такое «Мгновенный центр скоростей» в других словарях:
мгновенный центр скоростей — Точка плоской фигуры, скорость которой в данный момент времени равна нулю. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика… … Справочник технического переводчика
мгновенный центр скоростей — Точка плоской фигуры, скорость которой в данный момент времени равна нулю … Политехнический терминологический толковый словарь
мгновенный центр скоростей — instantaneous centre of velocity Точка звена, скорость которой относительно системы отсчета в данный момент времени равна нулю. Шифр IFToMM: 2.3.3 Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
мгновенный центр вращения — Точка неподвижной плоскости, поворотом вокруг которой плоская фигура перемещается из данного положения в положение, бесконечно близкое к данному. Примечание. В каждый момент времени мгновенный центр вращения совпадает с мгновенным центром… … Справочник технического переводчика
Мгновенный центр ускорений — Мгновенный центр ускорений при непоступательном движении точка, находящаяся в плоскости движения тела, ускорение которой в данный момент времени равно нулю. Положение мгновенного центра ускорений в общем случае не совпадает с положением… … Википедия
МГНОВЕННЫЙ ЦЕНТР ВРАЩЕНИЯ — точка плоской неизменяемой фигуры, совершающей непо ступат. движение в своей плоскости, скорость к рой в данный момент времени равна 0. М. ц. в. лежит на пересечении прямых, проведённых в разл. точках фигуры перпендикулярно векторам скоростей… … Большой энциклопедический политехнический словарь
Центр в физике — В механике понятие о Ц. или связано с понятием о симметрии (см. Ось) вокруг него, или с понятием о месте приложения равнодействующей некоторой совокупности сил, приложенных к твердому телу. В кинематике. При рассмотрении скоростей точек какой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Центр (физ.) — В механике понятие о Ц. или связано с понятием о симметрии (см. Ось) вокруг него, или с понятием о месте приложения равнодействующей некоторой совокупности сил, приложенных к твердому телу. В кинематике. При рассмотрении скоростей точек какой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
СТРУКТУРА МЕХАНИЗМОВ — см. также о словаре аксоид аналог скорости точки аналог углового ускорения звена а … Теория механизмов и машин
МЦС — Международная церковь саентологии религ. МЦС Мобильная цифровая связь ООО организация, связь МЦС многоцелевой самолёт авиа МЦС … Словарь сокращений и аббревиатур
Мгновенный центр скоростей
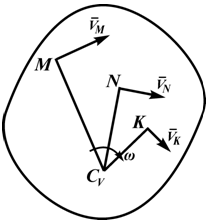
Простой и наглядный способ определения скоростей плоской фигуры основан на понятии о мгновенном центре скоростей (МЦС). Им называют точку подвижной плоскости, в которой расположена плоская фигура S и скорость которой в данный момент времени равна нулю.
Доказана теорема о том, что если тело движется не поступательно, то такая точка существует, и притом единственная. Из определения следует, что в общем случае в каждый момент времени МЦС находится в различных точках плоскости. При вращательном движении тела вокруг неподвижной оси, являющимся частным случаем плоскопараллельного движения, МЦС в любой момент времени расположен на оси вращения. Если же тело движется поступательно или мгновенно поступательно (скорости всех точек тела в данный момент времени равны по величине и совпадают по направлению), то МЦС находится на бесконечно большом расстоянии от любой точки тела. Выбрав в качестве полюса точку Р, которая является в данный момент времени МЦС, а значит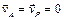 
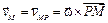
, из формулы (3.4) для определения скорости любой точки плоской фигуры найдем скорость точки М
. (3.8)
Следовательно, скорость любой точки тела в данный момент времени находим так же, как при вращении вокруг неподвижной оси, проходящей через МЦС и перпендикулярной плоскости движения. Таким образом, при плоскопараллельном движении скорость любой точки тела перпендикулярна отрезку, соединяющему эту точку с МЦС, а модуль скорости пропорционален расстоянию до МЦС
(3.9)
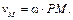
Угловая скорость плоской фигуры равна отношению скорости какой-либо ее точки к расстоянию от этой точки до МЦС
(3.10)
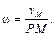
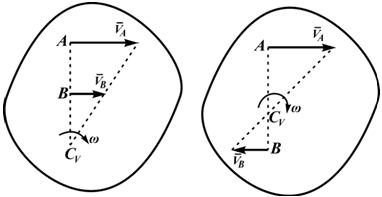
Способы определения положения мгновенного центра скоростей:
1) если известны направления скоростей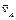 
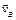
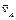
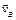
и 
точек А и В плоской фигуры, то МЦС (точку Р) определяют как точку пересечения перпендикуляров к скоростям и , проведенных из этих точек (рис. 3.3,а);
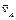
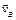
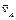
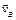
2) если скорости двух точек тела A и B известны по модулю, параллельны друг другу ( || ), и перпендикулярны прямой AB, то МЦС находят в точке пересечения прямой АВ с прямой, соединяющей концы векторов скоростей и (рис. 3.3,б,в);
3) при качении без скольжения одного тела по неподвижной поверхности МЦС находят в точке соприкосновения тел (рис. 3.3,г), так как при отсутствии скольжения скорость этой точки подвижного тела равна нулю;
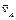
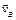
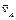
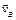
4) если скорости точек A и B тела и параллельны друг другу ( || ) и не перпендикулярны прямой АВ, то перпендикуляры к ним также параллельны друг другу. В этом случае МЦС находится в бесконечном удалении от точек A и B, движение тела является мгновенно поступательным, следовательно, скорости всех точек тела равны, а его угловая скорость в данный момент времени равна нулю.
С помощью МЦС плоскопараллельное движение можно представить не только как сложное, состоящее из поступательного и вращательного движений, но и как простое движение, состоящее из серии элементарных последовательных поворотов вокруг МЦС. Необходимо отметить, что положение МЦС в пространстве во все время движения меняется. Геометрическое место точек МЦС подвижного тела называют подвижной центроидой, а неподвижного тела – неподвижной центроидой. Таким образом, плоскопараллельное движение представляет собой качение без скольжения подвижной центроиды по неподвижной центроиде.
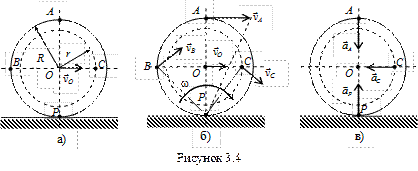
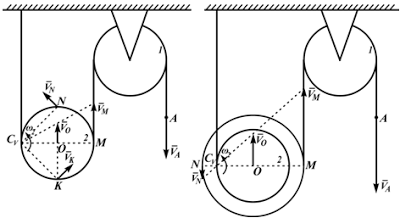
Пример 1. Колесо катится без скольжения по неподвижной прямой поверхности. Скорость точки O постоянна и равна 100 см/с (рис. 3.4,а).
Определить угловую скорость колеса, скорости точек A, B, C и ускорения точек A, C, P, если R = 50 см, r = 40 см.
Колесо совершает плоскопараллельное движение. Качение происходит без скольжения, следовательно, в данном случае точка касания колеса с неподвижной поверхностью – точка P – является МЦС. Определим угловую скорость колеса согласно формуле (3.10)
Зная расстояния от точек A, B и C до МЦС, можно найти их скорости по формуле (3.9)
Векторы скоростей точек колеса направлены перпендикулярно отрезкам, соединяющим их с МЦС (см. рис. 3.4,б). В соответствии с теоремой о проекциях скоростей двух точек тела на прямую, соединяющую эти точки, убеждаемся в правильности полученных результатов.
Перейдем к определению ускорений, для чего воспользуемся формулами (3.6) и (3.7). В качестве полюса выбираем точку O. Ускорение полюса равно нулю, так как эта точка движется равномерно и прямолинейно. Поэтому ускорения точек будут равны их ускорениям во вращательном движении вокруг полюса. Например, для точки А
.
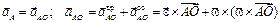
Дифференцируя по времени выражение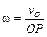 
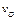
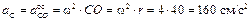
и учитывая, что OP = const и 
= const, получим 
Таким образом, ускорения всех точек, включая МЦС, состоят из осестремительных ускорений во вращении вокруг полюса О
;
и направлены от соответствующих точек к полюсу (см. рис 3.4,в).
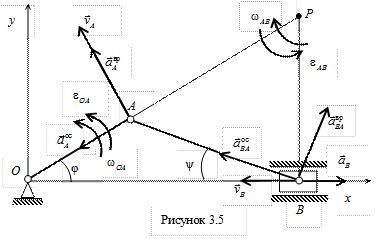
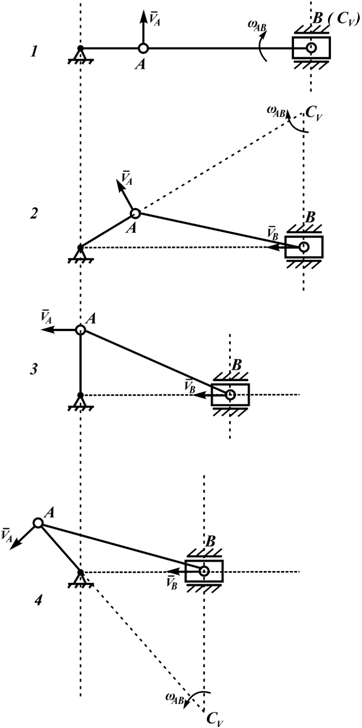
Пример 2. Кривошип ОА кривошипно-ползунного механизма, приведенного на рис. 3.5, вращается вокруг неподвижной оси с угловой скоростью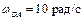 
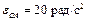
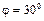
и угловым ускорением 
. Положение механизма определяется углом 
.
Найти угловую скорость и угловое ускорение шатуна АВ, а также скорость и ускорение ползуна B, если длина кривошипа ОА = 10 см, а длина шатуна АВ = 30 см.
Вначале определим скорость точки А кривошипа
Затем, зная направления скоростей точек А и В, найдем положение МЦС на пересечении перпендикуляров к скоростям этих точек – точку P. Для определения угловой скорости шатуна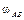 
и скорости точки В находим длины отрезков, соединяющих точки А и В с МЦС. Из теоремы синусов следует, что
Вычислим длины отрезков:
.
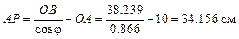
Теперь найдем искомые величины:
Определим ускорение точки В и угловое ускорение шатуна АВ. Здесь надо иметь в виду, что расстояние от точки А до МЦС не является постоянным и зависит от положения механизма, т.е. от времени. Поэтому продифференцировать по времени угловую скорость шатуна не представляется возможным. Поступим следующим образом. Для нахождения ускорения точки В воспользуемся векторным равенством (3.6)
и спроецируем его на оси координат xOy (см. рис. 3.5). При этом учтем, что вектор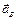 
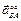
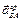
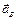
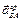
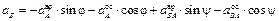
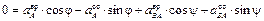
лежит на прямой ОВ, так как точка В движется прямолинейно, вектор 
направлен к полюсу А, а вектор 
перпендикулярен ему. Получим два алгебраических уравнения для определения величин и направлений ускорений и (вначале направляем искомые векторы произвольно):
;
.
Предварительно вычислим составляющие ускорения согласно формулам (3.7):
Знаки показывают, что направление ускорения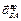 
совпадает с принятым, а направление – противоположно направлению, указанному на рис. 3.5. Зная ускорение 
, можно найти угловое ускорение шатуна
Вопросы для самоконтроля
1. Какое движение твердого тела называют плоскопараллельным?
2. На какие простейшие движения можно разложить плоскопараллельное движение?
3. Какие уравнения описывают плоскопараллельное движение?
4. Как определяют скорость произвольной точки плоской фигуры, если известна скорость полюса?
5. Какую точку плоской фигуры называют мгновенным центром скоростей (МЦС)?
6. Как распределены скорости точек тела по отношению к МЦС?
7. Какие существуют способы определения положения МЦС?
8. Как определяют ускорения произвольных точек тела, совершающего плоскопараллельное движение?
iSopromat.ru
Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.
Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.
В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.
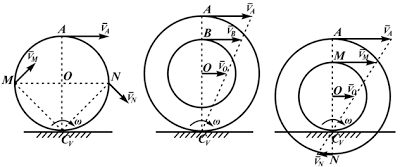
Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:
На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.
На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.
В этом случае МЦС находится в «бесконечности», т.е.
Формулы справедливы при отсутствии проскальзывания в точке CV.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Решение задач, контрольных и РГР
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Набор студента для учёбы
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку