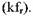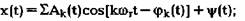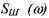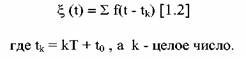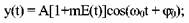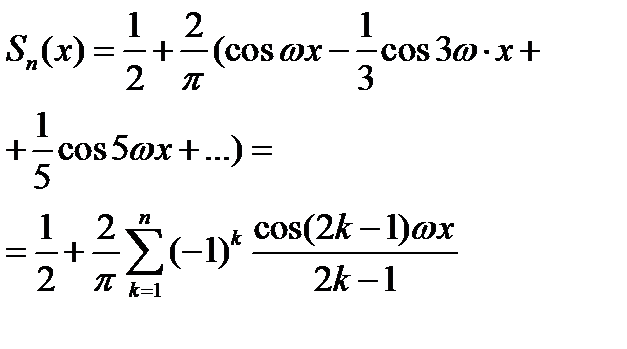На чем основана квазиполигармоническая модель процесса возбуждения колебаний
Свойства вибросигнала роторных агрегатов.
Представление вибросигнала полигармонической и квазиполигармонической моделями.
В роторных агрегатах одной из основных частот возбуждения вибрации является оборотная (роторная) частота, называемая в дальнейшем частотой вращения ротора:
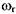
Таким образом, информативными параметрами в такой модели колебаний являются значения амплитуд дискретных составляющих спектра на частоте вращения ротора и ее гармониках и скорость их изменения при увеличении наработки механизма. Амплитуды колебаний на роторных частотах определяются чаще всего величиной дисбаланса, несоосностью валов, кинематическими погрешностями и отношением критической частоты вращения ротора к рабочей.
Помимо упомянутой выше вибрации, кратной частоте вращения ротора, в спектре вибросигнала роторного агрегата могут присутствовать такие характерные частотные составляющие, как
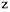
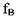
Практика вибродиагностики роторных агрегатов показала, что полигармоническая модель вибросигнала является лишь нулевым приближением в описании сложного колебательного процесса реального агрегата, хотя может с успехом использоваться в задачах локализации источников и в задачах диагностирования грубых дефектов типа разрушения лопаток турбины, деталей подшипников, поломки зубьев и т. п., вызывающих существенное увеличение уровня колебаний на определенных частотах. В работе реального агрегата абсолютное повторение с течением времени условий взаимодействия его деталей между собой и с внешней средой практически невозможно.
Погрешности изготовления и монтажа деталей, температурные изменения геометрических параметров деталей и зазоров в сочленениях, изменение вязкости смазки, искажение формы и качества поверхностей взаимодействующих деталей с наработкой, наконец, нестабильность оборотов вала двигателя, вызванная, например, нестабильностью частоты сетевого напряжения, и множество других случайных факторов приводят к флуктуациям амплитуд и размытию дискретных линий спектра полигармонических колебаний.
Более адекватной моделью процесса возбуждения колебаний является суперпозиция узкополосных случайных процессов с кратными средними частотами:

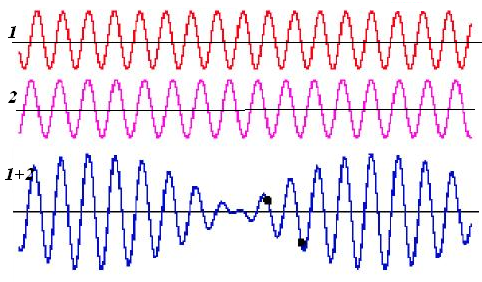
Энергетический спектр такого процесса (см. рис. 1 — 03) сосредоточен в узких полосах частот в окрестности кГг.
рассматриваемом диапазоне частот. Такая форма представления вибросигнала достаточно хорошо моделирует износ контактирующих поверхностей зубьев колес в редукторе, в подшипниках качения и т. п.
Соотношение энергии периодического и шумового компонентов является информативным параметром вибросигнала, широко используемым при формировании диагностических признаков состояния агрегата.
Импульсная модель акустического сигнала.
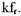
базирующаяся на представлении процессов возбуждения колебаний в роторных агрегатах в виде периодической последовательности импульсов определенной формы. Такая модель достаточно универсальна, так как она позволяет математически описать процессы возбуждения колебаний как в роторных механизмах типа зубчатого зацепления, подшипников качения и скольжения, турбинах, вентиляторах, циркуляционных и центробежных насосах, так и в поршневых машинах с механизмами циклического ударного действия.
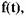
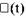
случайность одиночного импульса, которая заключается в том, что его амплитуда, длительность и момент появления могут быть, вообще говоря, случайными величинами.
В ряде практических моделей вибросигнала функционирующих механизмов имеет место периодическая последовательность импульсов, модулированных по амплитуде, при неизменной форме, длительности и частоты следования импульсов. Такой вид модуляции, называемой амплитудно-импульсной модуляцией (АИМ), наиболее часто используется для математического представления акустического сигнала.

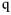

Для формирования диагностического признака используют обычно представление сигнала в достаточно узком диапазоне частот, например в зоне одной из гармоник основной частоты возбуждения механизма (зубцовой, винтовой, лопаточной и др.).
При этом представляют колебания в виде модуляции высокочастотного гармонического сигнала суммой гармонических же низкочастотных колебаний.
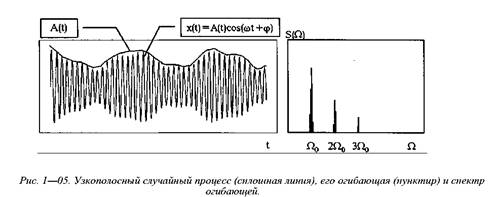
На рис. 1—05 приведен узкополосный случайный процесс (амплитудная модуляция), описываемый математическим выражением вида:
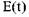
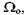
Выделение огибающей производится с помощью амплитудного детектора.
Назначение и возможности систем вибрационного мониторинга и диагностики роторного оборудования
Разнообразие дефектов, обнаруживаемых методами вибрационной диагностики, и сложность сигналов, порождаемых неисправностями и колебаниями деталей агрегатов, заставляет при выявлении и измерении
Назначение и возможности систем вибрационного мониторинга и диагностики роторного оборудования
Другие дипломы по предмету
Модель полигармонического возбуждения колебаний в роторных агрегатах является удобной формой представления спектра колебательного процесса, позволяющего сконцентрировать внимание лишь на определенных частотах kfB, кратных основной частоте возбуждения колебаний fB диагностируемого узла агрегата. Первичный процесс локализации источников повышенной виброактивности конструкции агрегата состоит как раз в выявлении потенциальных источников возбуждения, вызывающих колебания на данной частоте.
Практика вибродиагностики роторных агрегатов показала, что полигармоническая модель вибросигнала является лишь нулевым приближением в описании сложного колебательного процесса реального агрегата, хотя может с успехом использоваться в задачах локализации источников и в задачах диагностирования грубых дефектов типа разрушения лопаток турбины, деталей подшипников, поломки зубьев и т. п., вызывающих существенное увеличение уровня колебаний на определенных частотах. В работе реального агрегата абсолютное повторение с течением времени условий взаимодействия его деталей между собой и с внешней средой практически невозможно.
Погрешности изготовления и монтажа деталей, температурные изменения геометрических параметров деталей и зазоров в сочленениях, изменение вязкости смазки, искажение формы и качества поверхностей взаимодействующих деталей с наработкой, наконец, нестабильность оборотов вала двигателя, вызванная, например, нестабильностью частоты сетевого напряжения, и множество других случайных факторов приводят к флуктуациям амплитуд и размытию дискретных линий спектра полигармонических колебаний.
Более адекватной моделью процесса возбуждения колебаний является суперпозиция узкополосных случайных процессов с кратными средними частотами:
Рис. 2.3. Спектры полигармонического и квазиполигармонического процесса.
Энергетический спектр такого процесса (см. рис. 2.3.) сосредоточен в узких полосах частот в окрестности kfr.
При моделировании возбуждения колебаний в роторных агрегатах изменение состояния агрегата можно оценивать по изменению не только величин амплитуд спектральных составляющих, но и уровня шумового возбуждения ψ(t) с равномерным спектром Sш (ω) в рассматриваемом диапазоне частот. Такая форма представления вибросигнала достаточно хорошо моделирует износ контактирующих поверхностей зубьев колес в редукторе, в подшипниках качения и т. п.
Соотношение энергии периодического и шумового компонентов является информативным параметром вибросигнала, широко используемым при формировании диагностических признаков состояния агрегата.
Импульсная модель акустического сигнала.
Квазиполигармоническая модель колебательного процесса [1.1] мало что говорит о соотношении амплитуд спектра на частотах kfr. Эту информацию может дать модель, базирующаяся на представлении процессов возбуждения колебаний в роторных агрегатах в виде периодической последовательности импульсов определенной формы. Такая модель достаточно универсальна, так как она позволяет математически описать процессы возбуждения колебаний как в роторных механизмах типа зубчатого зацепления, подшипников качения и скольжения, турбинах, вентиляторах, циркуляционных и центробежных насосах, так и в поршневых машинах с механизмами циклического ударного действия.
Обозначая функцию, определяющую отдельный импульс, через f(t), можно представить периодическую последовательность импульсов в виде
Функция ξ(t) может быть как детерминированной, так и случайной, отражающей случайность одиночного импульса, которая заключается в том, что его амплитуда, длительность и момент появления могут быть, вообще говоря, случайными величинами.
В ряде практических моделей вибросигнала функционирующих механизмов имеет место периодическая последовательность импульсов, модулированных по амплитуде, при неизменной форме, длительности и частоты следования импульсов. Такой вид модуляции, называемой амплитудно-импульсной модуляцией (АИМ), наиболее часто используется для математического представления акустического сигнала.
В работающем агрегате в зависимости от характера физического процесса, протекающего в нем, возможны различные отклонения в последовательности импульсов, которые можно охарактеризовать модуляцией амплитуды, длительности или моментов появления импульсов, однако при функционировании оборудования с заданной функцией взаимодействия деталей, определяющейся кинематикой агрегата, наиболее часто встречается амплитудная модуляция, обусловленная разбросом величины силы взаимодействия его элементов в каких-то пределах (неоднородность структуры контактирующих поверхностей зубьев, приводящая к вариации пятна контакта колес зубчатого зацепления; неравномерность воздушного потока в зазоре, отклонение геометрических размеров лопаток турбины вследствие обгара, эрозии и др.). В то же время погрешность окружного шага или явление заедания в зубчатом зацеплении, изгибная деформация, приводящая к неравномерному размещению лопаток в диске или на рабочем колесе турбины, являются причиной возбуждения модулированных по фазе импульсных колебаний.
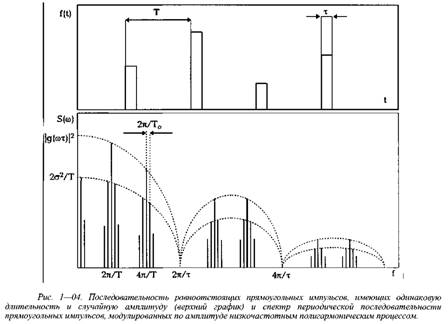
Рис. 2.4. Последовательность равноотстоящих прямоугольных импульсов, имеющих одинаковую длительность и случайную амплитуду (верхний график) и спектр периодической последовательности прямоугольных импульсов, модулированных по амплитуде низкочастотным полигармоническим процессом.
Для формирования диагностического признака используют обычно представление сигнала в достаточно узком диапазоне частот, например, в зоне одной из гармоник основной частоты возбуждения механизма (зубцовой, винтовой, лопаточной и др.).
Рис. 2.5. Узкополосный случайный процесс (сплошная линия), его огибающая (пунктир) и спектр огибающей.
При этом представляют колебания в виде модуляции высокочастотного гармонического сигнала суммой гармонических же низкочастотных колебаний.
На рис. 2.5 приведен узкополосный случайный процесс (амплитудная модуляция), описываемый математическим выражением вида:
y (t) = A [1+m·E (t)] ·cos (ω0t + φ0);
Выделение огибающей производится с помощью амплитудного детектора.[3]
2.7 Методика диагностирования зарождающихся дефектов
Дефекты контактирующих поверхностей и характер их проявления в виброакустическом сигнале.
Вибродиагностика базируется на анализе изменений свойств вибропроцессов, предполагая, что вибросигнал работающего агрегата содержит всю информацию о взаимодействии его деталей. Задача заключена в разработке алгоритмов извлечения из него информации о состоянии определенного узла и локализации возникающих неисправностей. Большой уровень помех и сравнительно малые изменения полезного сигнала определяют специфику поиска информативных диагностических признаков, чувствительных к развивающемуся дефекту и инвариантных к мешающим факторам. Лишь в исключительных случаях увеличение общего уровня вибросигнала свидетельствует о зарождении определенного дефекта. Как правило, существенное увеличение общего уровня вибрации или отдельных спектральных компонентов говорит лишь о грубых изменениях состояния диагностируемого агрегата, приводящих к потере его работоспособности. Локализация же развивающейся неисправности, еще не приведшей к развитому дефекту, определение степени развития зарождающегося дефекта и прогнозирование возможны лишь на основе исследований тонкой структуры виброакустического сигнала и связи его с кинематикой и динамикой агрегата.
Изучение свойств вибропроцессов роторных агрегатов, показало, что при появлении неисправности меняется структура сигнала, т. е. меняется соотношение между его компонентами или появляются новые. Это подтвержд
Периодические колебания



Отличительным признаком периодических колебаний является повторение колеблющейся величины через одинаковый промежуток времени, который называют периодом колебаний. Периодическим колебаниям бесконечно большой длительности соответствуют дискретные (линейчатые) спектры, состоящие из конечного или бесконечного множества отдельных спектральных линий. Простейшим видом периодических колебаний являются моногармонические колебания, при которых колеблющаяся величина изменяется по закону
Спектр моногармонического колебания содержит только одну наблюдаемую частоту (рис. 2.4). Полигармонический колебательный процесс (рис. 3.5) может быть представлен в виде суммы нескольких моногармонических колебаний с частотами, находящимися между собой в рациональном отношении:
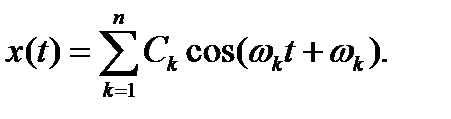
Форма графика изменения колеблющейся величины во времени в зависимости от соотношения параметров k гармоник позволяет провести классификацию процессов, разделяя их на прямоугольные, пилообразные, трапецеидальные и другие колебания.
Частный случай полигармонических колебаний – это бигармонические колебания, состоящие из суммы двух моногармонических колебаний (см. рис. 3.6):
угловые частоты которых ω1 и ω2 находятся между собой в рациональном отношении:
Вид бигармонического колебательного процесса зависит не только от соотношения между частотами и амплитудами обеих гармоник, но и от фазовых соотношений. При достаточной близости частот колебаний будут наблюдаться характерные биения процесса (рис.3.6), при которых его полуразмах
Рис. 3.6. Биения ротора электродвигателя
Таким образом, биение– это результат сложения двух колебаний с близкими частотами.
Преимущества полигармонической моделивозбуждения колебаний в том, что она позволяет сконцентрировать внимание лишь на определенных частотах kfв , кратных основной частоте возбуждения колебаний fв диагностируемого узла, поскольку процесс локализации источников повышенной виброактивности агрегата состоит в выявлении источников возбуждения, вызывающих колебания на данной частоте.
Квазиполигармоническая модельпроцесса возбуждения колебаний основана на представлении колебаний в виде суперпозиции узкополосных случайных процессов с кратными средними частотами. Квазиполигармоническая модель более адекватно, чем полигармоническая описывает процесс возбуждения колебаний. Размытие линий спектра квазиполигармонической модели колебаний по отношению к дискретным составляющим полигармонической модели не является недостатком.