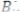на каком положении основано деление отрезка прямой в заданном отношении

3.6 Деление отрезка прямой в заданном отношении

Если в пространстве точка делит отрезок прямой в каком-либо отношении, то на чертеже проекции точки делят одноименные проекции отрезка в таком же отношении (рис. 49).

Известно: AB – прямая общего положения; ab проекция AB ; .

Доказать: .

Рисунок 49 – Схема деления отрезка прямой в заданном отношении

. Рассмотрим прямоугольные треугольники

подобны. Отсюда: , заменяя , , получим .

Пример: разделить отрезок АB в отношении .

Рисунок 50 – Эпюр, деление отрезка в заданном отношении

Используем теорему Фалеса.

3.7 Проецирование углов

Если две стороны какого-либо угла параллельны плоскости проекций, то угол на эту плоскость проецируется без искажения (рис. 51).

Если одна сторона острого (тупого) угла параллельна плоскости проекций, то острый угол проецируется в острый угол, но меньшего размера, а тупой угол в тупой, но большего размера.

Теорема о частном случае проецирования прямого угла

Если одна из сторон прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется в натуральную величину без искажения (рис. 52).

Известно, что ; . Доказать, что

3 Для нахождения натуральной величины отрезка AB и его отношения можно применить метод прямоугольного треугольника (рис. 21).

Доказательство: – из условия; ; ; – т. к. она перпендикулярна пересекающимся прямым.

Рисунок 51 – Наглядное изображение и эпюр, проецирование угла

Рисунок 52 – Наглядное изображение, проецирования прямого угла

; .

Следовательно, . Отсюда: ;

Теорема дает нам право на проведение перпендикуляра к прямой, если она параллельна плоскости проекций.

Прямая общего положения и горизонтальная прямая уровня перпендикулярны, если перпендикулярны их горизонтальные проекции (рис. 53, а ).

Прямая общего положения и фронтальная прямая перпендикулярны, если перпендикулярны их фронтальные проекции (рис. 53, б ).

Источник

Проецирование отрезка и деление его в данном отношении

Наглядное изображение отрезка АВ прямой и его ортогонального проецирования на плоскость Р показано на рисунке 2.1. Рассмотрим ортогональное проецирование отрезка АВ с учетом свойств параллельного проецирования (1.2). Параллельные проецирующие прямые Аа_р и Вb_Р, проведенные из точек А и В прямой, образуют проецирующую плоскость Q, пересекающуюся с плоскостью проекций Р. Линия пересечения плоскостей Р и Q проходит через проекции а_р и b _р точек А и В на плоскости проекций Р. Эта линия и является единственной проекцией прямой на плоскости проекций Р.

Между длинами отрезка АВ прямой и его проекции арbр имеется зависимость |apb _р| = | АВ| cosφ, где φ — угол между отрез

ком и плоскостью проекций. При φ=0 отрезок проецируется в натуральную величину; при φ=90° отрезок проецируется в точку. В остальных случаях длина проекции отрезка меньше длины самого отрезка.

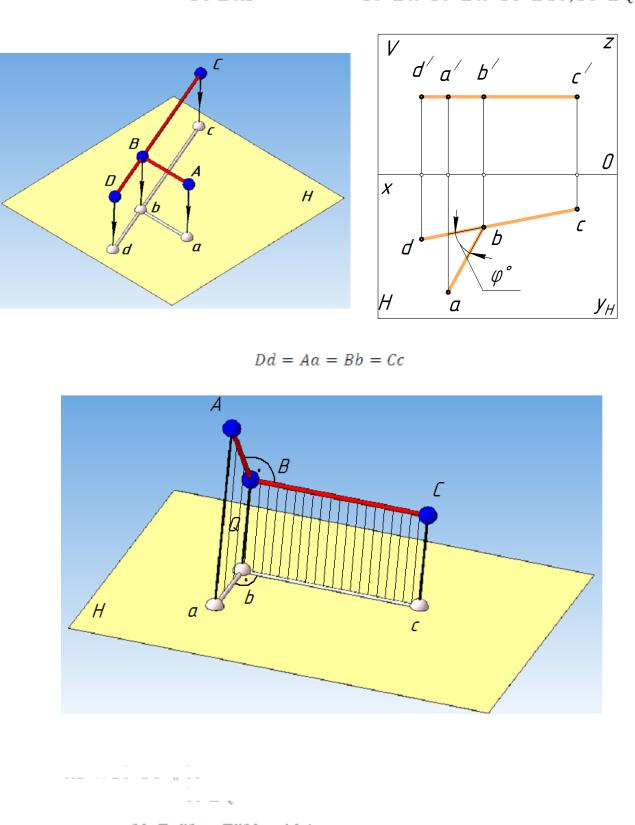
Наглядное изображение проецирования отрезка АВ прямой на две плоскости проекций в системе V, Н показано на рисунке 2.2, чертеж — на рисунке 2.3.

Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. Например, точка D (см. рис. 2.1) принадлежит прямой АВ, ее проекция d_p — проекция арbр. На рисунке 2.3 точка с проекциями d’ и d принадлежит прямой с проекциями a’b’, ab.

Если точка на отрезке делит его длину в данном отношении, то проекция точки делит длину одноименной проекции отрезка в том же отношении (см. рис. 1.8). Например, на рисунке 2.1 отношение | АВ| / | DB | = | a_pd_p| / | dpbp|. Для рисунка 2.3 — отношения | a’d’ | / | d’b’| и |ad| / | ab | равны отношению | AD | / | DB |.

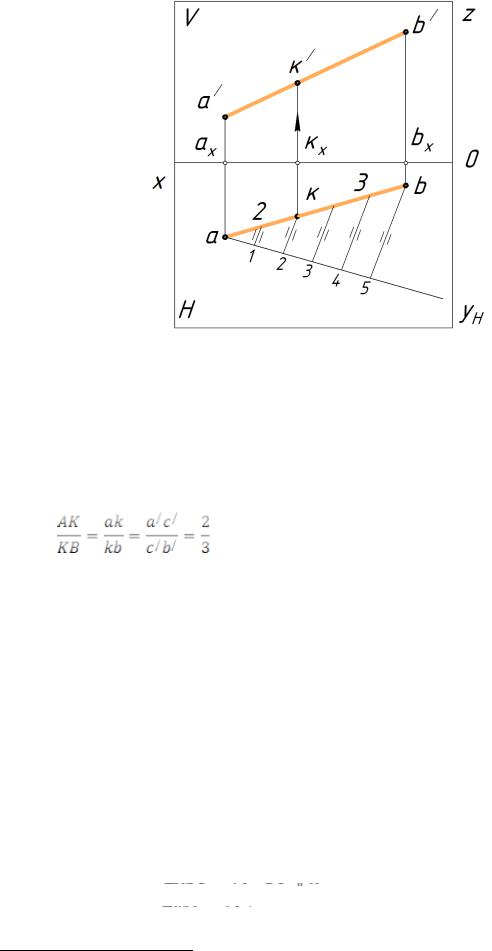
Пример построения на чертеже проекций к’ и к точки К, делящей отрезок с проекциями a’b’, ab в отношении 1:3, показан на рисунке 2.4.

Источник

Как осуществить деление отрезка?

Когда существуют условия деления отрезка в определенном отношении, необходимо уметь определять координаты точки, служащей разделителем. Выведем формулу для нахождения этих координат, поставив задачу на плоскости.

Деление отрезка в заданном соотношении: координаты точки, делящей отрезок в заданном отношении, a-b точка

Определение координат точки, делящей отрезок в заданном отношении, на плоскости

Перед тем, как приступить к решению поставленной задачи, немного раскроем смысл заданного условия: «точка С, делящая отрезок АВ в отношении λ». Во-первых, это выражение свидетельствует о том, что точка С лежит на отрезке АВ (т.е. между точками А и В). Во-вторых, понятно, что согласно заданному условию отношение длин отрезков АС и СВ равно λ. Т.е. верно равенство:

Ну и совсем очевидный факт, что если λ = 1, то точка С является серединой отрезка АВ.

Определение координат точки, делящей отрезок в заданном отношении, в пространстве

Точка С делит отрезок АВ в отношении λ. Необходимо определить координаты точки С.

Известно, что центром тяжести любого треугольника является точка пересечения его медиан (пусть это будет точка М). Каждая из медиан делится точкой М в отношении 2 к 1, считая от вершины. Исходя из этого, найдем ответ на поставленный вопрос.

Найдем координаты точки D. Так как AD – медиана, то точка D – середина отрезка ВС. Тогда, используя формулу нахождения координат середины отрезка, получим:

Теорема Фалеса и деление отрезка в заданном отношении

Давно о геометрии не говорили, а о теореме ФАлеса (или ФалЕса?) вообще мало говорят. Хотя она весьма полезна. Начнем с формулировки, которая весьма не вразумительна, чем и объясняется не популярность данной теоремы.

Мутно, долго, не понятно. Мне больше нравится другая формулировка. Тоже не понятно, но элегантно и коротко. Задачи, которые решаются с помощью данной теоремы, довольно специфичны. Но есть одна задача на построение, которую можно встретить в реальной жизни. Это задача о делении отрезка в заданном отношении.

Суть вопроса: Дан отрезок. Его нужно поделить на два куска, чтобы их длины относились, как 2 : 5. Кусков может быть сколько угодно и отношение, может быть каким угодно. Алгебраически задача решается крайне легко: находим общее количество частей (2 + 5 = 7), делим длину отрезка на общее количество частей, находим длину каждого куска.

Но алгебраическое решение не всегда прокатывает. Например, мы не можем найти длину отрезка, или при делении получаются не целые числа. Тогда можно воспользоваться геометрическим способом. Во-первых, проводим луч из конца отрезка. Любой, в любую сторону.

Дальше, на этом луче от точки А откладываем 7 (общее количество частей) равных отрезков. Последнюю получившуюся точку — J соединяем с точкой В, а затем через каждую точку луча проводим прямую параллельную JB.

Таким образом, мы разделили отрезок АВ на 7 равных частей (по теореме Фалеса). Отсчитываем две части и ставим точку. Получаем: AK : KB = 2 : 5.

Вот таким простым образом, вы можете поделить свою комнату с соседом в любом отношении. Если вам кажется, что построение такого количества параллельных прямых дело сложное, то подумайте о перпендикулярах.

Источник

Деление отрезка в данном отношении, координаты, примеры, решения.

В этой статье мы разберемся с нахождением координат точки, которая делит некоторый отрезок в заданном отношении. Сначала мы получим формулы для нахождения координат такой точки по координатам концов отрезка. После этого приведем подробные решения нескольких характерных примеров.

Навигация по странице.

Вывод формул для нахождения координат точки, делящей отрезок в данном отношении, на плоскости.

Начнем с постановки задачи на плоскости.

Поставленная задача может быть решена с помощью векторов.

В силу операции сложения векторов можно записать равенства и . Их мы используем в следующем абзаце.

Так как точка С делит отрезок АВ в соотношении , то , откуда . Векторы и лежат на одной прямой и имеют одинаковое направление, а выше мы отметили, что , поэтому, по определению операции умножения вектора на число справедливо равенство . Подставив в него , имеем . Тогда равенство можно переписать как , откуда в силу свойств операций над векторами получаем .

Осталось вычислить координаты вектора , выполнив необходимые операции над векторами и в координатах. Так как и , то , следовательно, .

Координаты точки, которая делит отрезок в заданном отношении, в пространстве.

Теперь рассмотрим задачу нахождения координат точки, делящей отрезок в данном отношении, не на плоскости, а в трехмерном пространстве.

Нахождение координат точки, делящей отрезок в данном отношении, примеры и решения.

Пришло время применить полученные формулы при нахождении координат точки, делящей отрезок в заданном отношении. Рассмотрим решения наиболее часто встречающихся задач по этой теме.

.

В данном примере . Так как точка С делит отрезок АВ в данном отношении, то справедливы формулы и , из которых получаем и соответственно. Подставляем значения из условия и вычисляем искомые координаты точки А :

.

Одной из самых характерных задач, в которой приходится вычислять координаты точки, делящей отрезок в заданном соотношении, является задача на нахождение центра тяжести треугольника.

Осталось вычислить искомые координаты центра тяжести треугольника:

.

Источник