на каком языке написать калькулятор
Как написать программу-калькулятор
Добавьте в код 4 переменных, которые будут сохранять числа, введенные пользователем и определять режим. Например:
var
a, b, c: real; //числа, которые вводит пользователь
d: integer; //действие калькулятора
Созданные переменные можете внести как и в protected, так и в private. Теперь к каждой цифровой кнопке обработайте событие OnClick. Для всех цифр код будет идентичен:
procedure TForm1.Button1Click(Sender: TObject);
begin
Panel1.Caption:=Panel1.Caption+’число’
end;
Замените «число» на название кнопки (если это цифра 0, то Panel1.Caption+’0′).
Переменная d имеет формат integer и будет содержать соответствующее числовое значение какого-либо действия. Если будет осуществляться умножение, то можно задать действию значение 1, если деление — значение 2, если сложение — значение 3, и т. д. Для действия умножения код будет иметь вид:
procedure TForm1.ButtonMultiplyClick(Sender: TObject); //действие умножения
begin
a:=StrToFloat(Panel1.Caption); //после нажатия кнопки сохраняется значение переменной a
d:=1; //переменной действия задается соответствующее значение
Panel1.Caption:=»;
end;
Для обработки значения »=» необходимо сделать условие case и поочередно рассматривать каждое действие:
procedure TForm1.ButtonClick(Sender: TObject);
begin
case d of
1: begin //если d = 1, т. е. нажимается кнопка умножения, то происходит соответствующее действие
b:=StrToFloat(Panel1.Caption);
c:=a*b;
Panel1.Caption:=FloatToStr(c);
end;
2: begin
a:=StrToFloat(Panel1.Caption);
c:=a/b;
Panel1.Caption:=FloatToStr(c);
…
Простой калькулятор на JavaScript
Сегодня сделаем простейший калькулятор на JavaScript, но не просто так, а с умыслом. Позднее мы представим, что мы тестировщики, и попробуем протестировать этот калькулятор. Вернее, не протестировать, а дико сломать.
Что делаем
На старте у нас будет самый простой калькулятор, который сможет только складывать, вычитать, умножать и делить два числа. Этого уже будет достаточно, чтобы потренироваться и в коде, и в дальнейшем тестировании.
Логика работы
Так как это простой калькулятор, то поступим так:
Размещаем кнопки и поля ввода на странице
Разместим кнопки с полями на странице, а потом будем писать скрипт.
Обрабатываем нажатия на кнопки математических действий
Сейчас у нас есть 4 кнопки, но нажимать их бесполезно — всё равно ничего не произойдёт, потому что нет обработчиков нажатий. Но что нам прописывать в обработчике?
Первый вариант — привязать к каждой кнопке свою функцию, а потом для каждой операции выполнять свои действия внутри этого обработчика. Но раз у нас есть кнопка «Посчитать», то нам придётся при нажатии на неё из этих четырёх функций вытаскивать действие и нужные команды, запоминать выбранное и как-то использовать в вычислениях. Сложно и громоздко.
Второй вариант — просто записывать в какую-то переменную, какая кнопка была нажата. А потом, при нажатии «Посчитать», просто смотреть в эту переменную и выполнять соответствующее действие. Так и поступим.
👉 Воспользуемся хитростью, про которые многие забывают: в обработчике onclick необязательно писать только функцию — туда можно отправить любую JS-команду. Главное, не забыть потом в скрипте предусмотреть эту переменную, которую мы используем.
Пишем скрипт
Сам скрипт тоже будет простой:
Сразу привяжем функцию func() к нажатию на кнопку «Посчитать»:
Выводим результат
Сейчас в скрипте есть проблема: он всё считает, но ничего не выводит. А всё потому, что мы не предусмотрели на странице место для вывода. Исправим это и добавим строчку в скрипт.
Это — добавим на страницу после кнопки с расчётом:
А это — в функцию func(), чтобы она сразу отправляла результат на страницу:
Собираем всё вместе и смотрим результат
Отлично, калькулятор работает и складывает всё как нужно! Мы выполнили свою задачу — быстро запилили калькулятор на JavaScript, можно закрывать задачу в таск-трекере и браться за новую.
Что дальше
Дальше мы этот код отправим тестировщикам — вряд ли они в нём найдут что-то критичное или вообще какие-то ошибки, но правила есть правила. А если тестировщики тут что-то найдут, мы обязательно расскажем об этом в новой статье.
Попробуйте сами побыть тестировщиком и протестировать эту программу, а результатами тестирования поделитесь в комментариях.
Пишем свой парсер математических выражений и калькулятор командной строки
Примечание: полный исходный код проекта можно найти здесь.
Вы когда-нибудь задавались вопросом, как цифровой калькулятор получает текстовое выражение и вычисляет его результат? Не говоря уже об обработке математических ошибок, семантических ошибок или работе с таким входными данными, как числа с плавающей запятой. Лично я задавался!
Я размышлял над этой задачей, проводя инженерные разработки для моей магистерской работы. Оказалось, что я трачу много времени на поиск одних и тех же физических единиц измерения, чтобы проверить преобразования и правильность своих вычислений.
Раздражение от монотонной работы помогло мне вскоре осознать, что единицы и их преобразования никогда не меняются. Следовательно, мне не нужно каждый раз искать их, достаточно сохранить информацию один раз, а затем спроектировать простой инструмент, позволяющий автоматизировать проверку преобразований и корректности!
В результате я написал собственный небольшой калькулятор командной строки, выполняющий парсинг семантического математического выражения и вычисляющий результат с необходимой обработкой ошибок. Усложнило создание калькулятора то, что он может обрабатывать выражения с единицами СИ. Этот небольшой «побочный квест» значительно ускорил мой рабочий процесс и, честно говоря, я по-прежнему ежедневно использую его в процессе программирования, хотя на его создание потребовалось всего два дня.
Примечание: спроектированный мной парсер выражений является парсером с рекурсивным спуском, использующим подъём предшествования. Я не лингвист, поэтому незнаком с такими концепциями, как бесконтекстная грамматика.
В этой статье я расскажу о своей попытке создания настраиваемого микрокалькулятора без зависимостей, который может парсить математические выражения с физическими единицами измерения и ускорить ваш процесс вычислений в командной строке.
Я считаю, что это не только любопытное, но и полезное занятие, которое может служить опорной точкой для создания любой другой семантической системы обработки математических выражений! Этот проект позволил мне разрешить многие загадки о принципах работы семантических математических программ. Если вы любите кодинг и интересуетесь лингвистикой и математикой, то эта статья для вас.
Примечание: разумеется, я понимаю, что существуют готовые библиотеки для решения подобных задач, но это показалось мне любопытным проектом, для которого у меня уже есть хорошая концепция решения. Я всё равно решил реализовать его и очень доволен результатом. Примерами подобных программ являются insect, qalculate!, wcalc. Важное отличие моего решения заключается в том, что программа не требует «запуска», а просто работает из консоли.
Мой первый калькулятор командной строки
Основная задача калькулятора командной строки — парсинг человекочитаемого математического выражения с единицами измерения, возврат его значения (если его возможно вычислить) и указание пользователю на место, где есть ошибка (если вычислить его невозможно).
В следующем разделе я объясню, как на стандартном C++ в примерно 350 строках кода можно реализовать изящный самодельный калькулятор командной строки.
Чтобы алгоритм и процесс были нагляднее, мы будем наблюдать за следующим примером математического выражения:
результат которого должен быть равен 1,35 м.
Примечание: я использую квадратные скобки, потому что bash не любит круглые. Тильды эквивалентны знакам «минус», их нужно писать так, чтобы отличать от бинарного вычитания.
Синтаксис математических выражений с единицами измерения
Вычисляемое математическое выражение должно быть представлено как однозначно интерпретируемая строка символов. Для вычисления выражения нам нужно ответить на ряд важных вопросов:
Представление чисел и единиц измерения
Чтобы различные операции могли работать с парами «число-единица измерения», нужно задать их структуру и операторы. В следующем разделе я вкратце расскажу, как реализовать такие пары «число-единица измерения».
Единицы измерения СИ — простая реализация на C++
В международной системе единиц физические величины выражаются как произведение 7 основных единиц: времени, длины, массы, электрического тока, термодинамической температуры, количества вещества и силы света.
Каждую физическую величину можно создать из произведения степеней этих единиц. Мы называем полную сложную производную единицу «размерностью». Создадим структуру, отражающую этот факт, сохранив в ней вектор степеней, связанный с каждой основной единицей:
Мы можем задать каждую основную единицу как константу типа unit:
Зададим набор перегруженных операторов для структуры единиц. Разные единицы можно умножать/делить, но нельзя прибавлять/вычитать. При сложении/вычитании одинаковых единиц получается та же единица. Единицу без размерности нельзя использовать как степень, но единицу можно возвести в степень:
Пары значений «число-единица»
Числа, связанные с единицами, называются «значениями» и задаются следующим образом:
Аналогично единицам мы зададим набор перегруженных операторов, действующих между значениями и возвращающих новое значение:
Производные единицы как скомбинированные основные единицы
Имея строку, представляющую единицу или другую физическую величину, мы можем извлечь пару «число-единица» при помощи таблицы поиска. Значения создаются умножением основных единиц и сохраняются в map с ссылкой по символу:
Если задать, что некоторые величины являются безразмерными, то можно включить в таблицу поиска и математические константы.
Примечание: скомбинированные единицы обычно представляются неким «ключом» или строкой, которые люди могут понимать по-разному. В отличие от них, таблицу поиска легко модифицировать!
Примечание: оператор ^ в таблице поиска требует заключения в скобки из-за его низкого порядка предшествования.
Парсинг выражений
Для своего калькулятора я задал пять компонентов выражения: числа, единицы, операторы, скобки и особые символы.
Каждый символ в допустимом выражении можно отнести к одной из этих категорий. Следовательно, первым шагом будет определение того, к какому классу принадлежит каждый символ, и сохранение его в виде, включающем в себя эту информацию.
Примечание: «особые» символы обозначают унарные операторы, преобразующие значение. Примеры кода написаны на C++ и используют стандартную библиотеку шаблонов.
Мы зададим «класс парсинга» при помощи простого нумератора и зададим «кортеж парсинга» как пару между символом и его классом парсинга. Строка парсится в «вектор парсинга», содержащий упорядоченные кортежи парсинга.
Мы создаём вектор парсинга, просто сравнивая каждый символ со множеством символов, содержащихся в каждом классе.
Структура нашей основной программы заключается в сжатии выражения, построении вектора парсинга и передаче его в вычислитель, возвращающий вычисленное выражение:
Для нашего примера выражения это будет выглядеть так:
Распарсенный пример выражения. Каждый символ в строке может быть отнесён к конкретной категории. Числа обозначены красным, единицы оранжевым, операторы синим, скобки фиолетовым, а особые символы — зелёным.
С самым лёгким мы закончили. Создан вектор парсинга из входящих данных командной строки и теперь мы можем оперировать с числами, связанными со значениями.
Как вычислить вектор парсинга, чтобы получить единичное значение?
Вычисление выражений
Нам осталось вычислить вектор парсинга, для чего требуется информация о структуре семантических математических выражений.
Здесь можно сделать следующие важные наблюдения:
Одновременно внутри рекурсивным образом вычисляются скобки, чтобы свести их к одному значению.
В общем случае это означает, что вектор парсинга можно вычислить при помощи рекурсивной функции, возвращающей пару «число-единица».
Рекурсивная функция вычисления вектора парсинга
Рекурсивная функция eval описывается следующим процессом:
Создание упорядоченной последовательности значений и операторов
Начнём с определения функции eval, получающей дополнительный параметр n, обозначающий начальную точку:
Примечание: пустой вектор парсинга возвращает безразмерное единичное значение и вектор парсинга не может начинаться с оператора.
Мы итеративно проходим по строке, отслеживая начальную и конечную точку текущей наблюдаемой последовательности. Когда мы встречаем скобку, то находим конечную точку скобки и вызываем функцию вычисления для внутреннего выражения:
Это приведёт к рекурсии, пока не будет найдено выражение вектора парсинга, не содержащее скобок, а значит, состоящее из сбалансированной последовательности значений и операторов.
При вычислении внутреннего выражения скобки возвращается некое значение. После уничтожения всех скобок останется только сбалансированная последовательность значений и операторов.
Операторы можно добавлять напрямую, а значения задаются комбинацией чисел, единиц и унарных операторов. Мы можем создать значение, найдя последовательность идущих друг за другом кортежей парсинга, представляющих её, и построив его соответствующим образом:
Мы конструируем значения из их последовательности кортежей парсинга, выявляя числовые компоненты, единицы и унарные операторы.
Создание пар «число-единица» и унарные операторы
Так как этот калькулятор поддерживает представление в числах с плавающей запятой, значение может состоять и из предэкспоненты, и из степени. Кроме того, обе эти величины могут иметь знак.
Знак извлекается как первый символ, за которым следует последовательность чисел. Значение извлекается при помощи stof:
), потому что так проще отличать его от бинарного оператора вычитания.
Далее мы проверяем наличие записи с плавающей запятой и повторяем это, чтобы получить знак и величину степени:
Наконец, мы извлекаем оставшуюся единицу как строку и получаем соответствующее значение. Применяем оставшиеся в конце унарные операторы и возвращаем окончательный вид значения:
Этот процесс сводит все комбинации унарных операторов, чисел и единиц к структурам значений, с которыми можно оперировать при помощи бинарных операторов:
Здесь вы видите, как выражение с унарным оператором сводится к значению.
Примечание: позиция передаётся функции создания, чтобы была известна абсолютная позиция в выражении для обработки ошибок.
Сжатие упорядоченной последовательности значений и операторов
Наконец, у нас получилась сбалансированная последовательность значений и бинарных операторов, которую мы можем сжать, используя правильный порядок операций. Два значения, связанные стоящим между ними оператором, можно сжать при помощи простой функции:
Чтобы сжать всю сбалансированную последовательность, мы итеративно обходим вектор парсинга по разу для каждого типа оператора в правильном порядке и выполняем бинарные вычисления. Стоит заметить, что умножение и деление могут происходить одновременно, как и сложение с вычитанием.
Получаем окончательный результат по нулевому индексу и возвращаем его.
Скобки вычисляются рекурсивно, как внутренне сбалансированная последовательность значений и операторов. После устранения всех скобок из основного выражения возвращается окончательное значение.
Примечание: эта рекурсивная структура отражает древовидную природу семантики математического выражения.
Результаты и выводы
Описанная выше структура была обёрнута в простой инструмент командной строки, который я назвал «dima» (сокращённо от «dimensional analysis»). Полный исходный код можно найти здесь.
Этот простой калькулятор командной строки будет правильно вычислять выражения с единицами измерения.
Единицы правильно комбинируются и раскладываются:
одновременно позволяя быстро узнавать значения констант:
При необходимости таблицу поиска выражений с единицами можно модифицировать.
Можно расширить эту систему, добавив способ задания функций/преобразований с именами.
Ещё одно потенциальное улучшение: можно добавить некий буфер вычислений, при помощи оператора присваивания сохраняющий переменные в новом словаре, доступ к которому можно получить при других последующих вычислениях. Однако для такого сохранения состояния потребуется запись в файл или запуск процесса.
Этот семантический математический парсер можно полностью преобразовать и создать другие полезные математические программы.
Например, можно попробовать алгебраически преобразовывать выражения с переменными, чтобы находить более изящное представление на основании какого-нибудь способа оценки (длины, симметрии, повторяющихся выражений и т.д.)
Ещё одной возможной вариацией может стать вспомогательная функция дифференцирования, использующая алгоритмическую природу производных.
На правах рекламы
Наша компания предлагает виртуальные серверы в аренду для любых задач и проектов, будь то серьёзные выслечения или просто размещение блога на WordPress. Создавайте собственный тарифный план в пару кликов и за минуту получайте готовый сервер, максимальная конфигурация бьёт рекорды — 128 ядер CPU, 512 ГБ RAM, 4000 ГБ NVMe!
Тестируем и исправляем калькулятор на JavaScript
В нём много ошибок, но мы их пофиксим
Эта статья — продолжение истории про калькулятор на JavaScript. В предыдущих частях мы:
Теперь наш калькулятор будут смотреть инженеры по тестированию — постараются найти в нём ошибки логики, поведения, вычислений и прочие неявные моменты.
👉 В этой статье не будет автотестов, юнит-тестов, API-тестов и интеграционных тестов. Это всё нужные инструменты, но задача тестировщика, в частности, — выбрать правильный инструмент тестирования.
Если у него в работе очень простая программа (как наш калькулятор), то нет смысла городить автоматизацию и делать тесты ради тестов. Иногда можно и вручную всё проверить и получить точно такой же результат.
Базовое тестирование
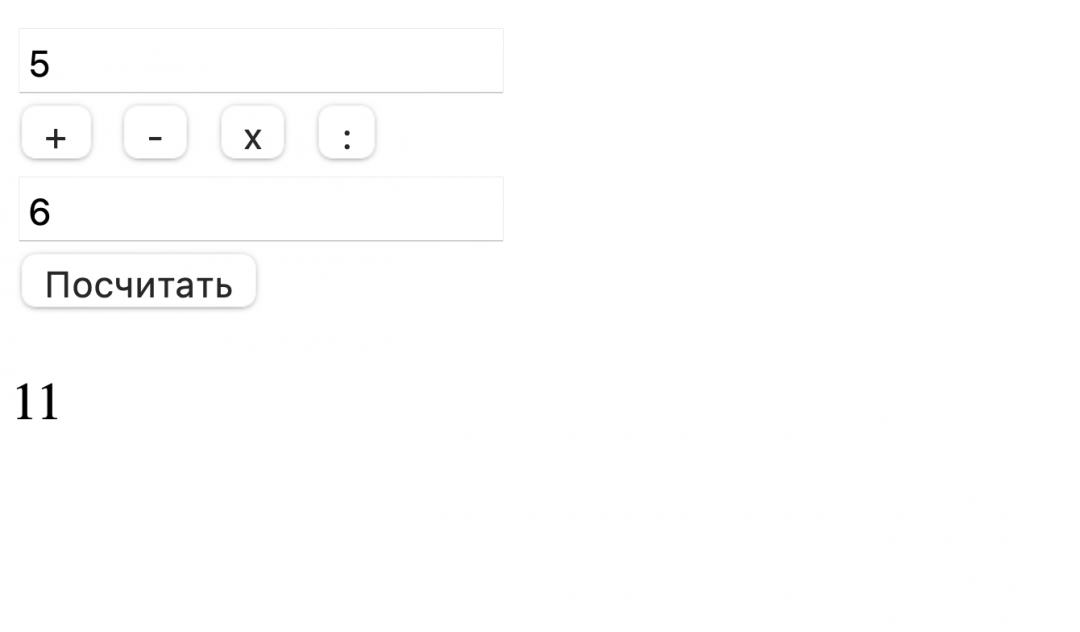
Первое, что мы делаем, — проверяем, а как вообще ведут себя кнопки математических действий и делают ли они то, что нужно. Возьмём два числа — 12 и 5 — и сравним результаты всех действий с тем, что даёт калькулятор:
Отрицательные числа тоже отображаются и считаются правильно.
Тестируем большие числа
У компьютеров есть нюанс: любые переменные имеют ограничения по размеру числа. Например, если на переменную выделено 16 бит, то максимальное число, которое можно в нее положить, — 65 536. Число на единицу больше уже потребует 17 бит, а мы столько не выделяли.
Мы хоть и разработчики этого калькулятора, но мы не помним, какое число имели в виду, когда заводили переменную. Может быть, это решение за нас принял JavaScript. Поэтому нужно проверить, не сломается ли наш калькулятор от больших чисел.
Пробуем: 123 456 789 × 2 = 246 913 578 — верно
А вот необычный эксперимент:
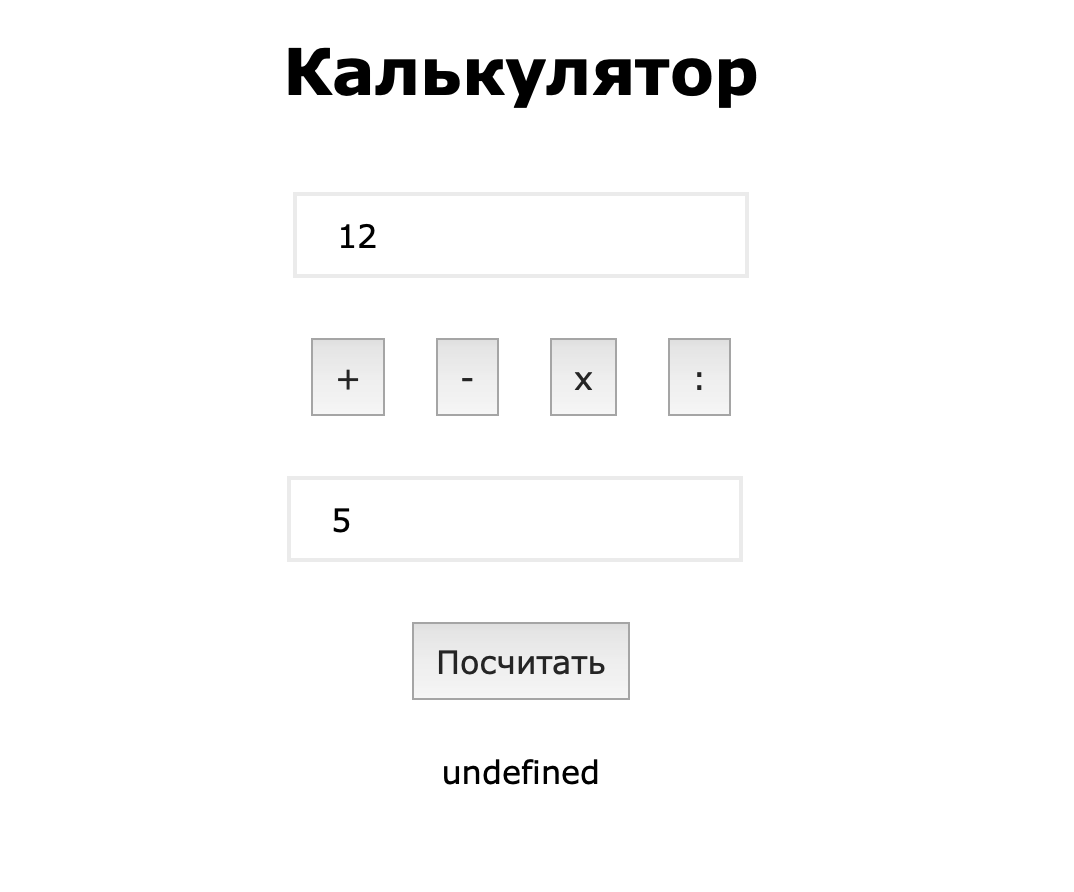
12 345 678 901 234 567 × 1 = 12 345 678 901 234 568
Ух ты! Мы умножили большое число на единицу, а в ответе появилась ошибка. Это значит, что настолько длинные числа за раз наш калькулятор уже обработать не в состоянии.
❌ Неправильно обрабатываются 17-значные числа и те, которые больше них.
А если мы попробуем получить 17-значное число в ответе, интересно, оно тоже будет с ошибкой?
Да, в ответе тоже неверное число — 8 × 4 = 32, поэтому в конце должно стоять 2, а не 0. Пишем баг:
❌ Если в ответе получается 17-значное число или более — ответ точно неверный.
При этом деление на 16-значное число работает верно:
Тестирование математических трюков
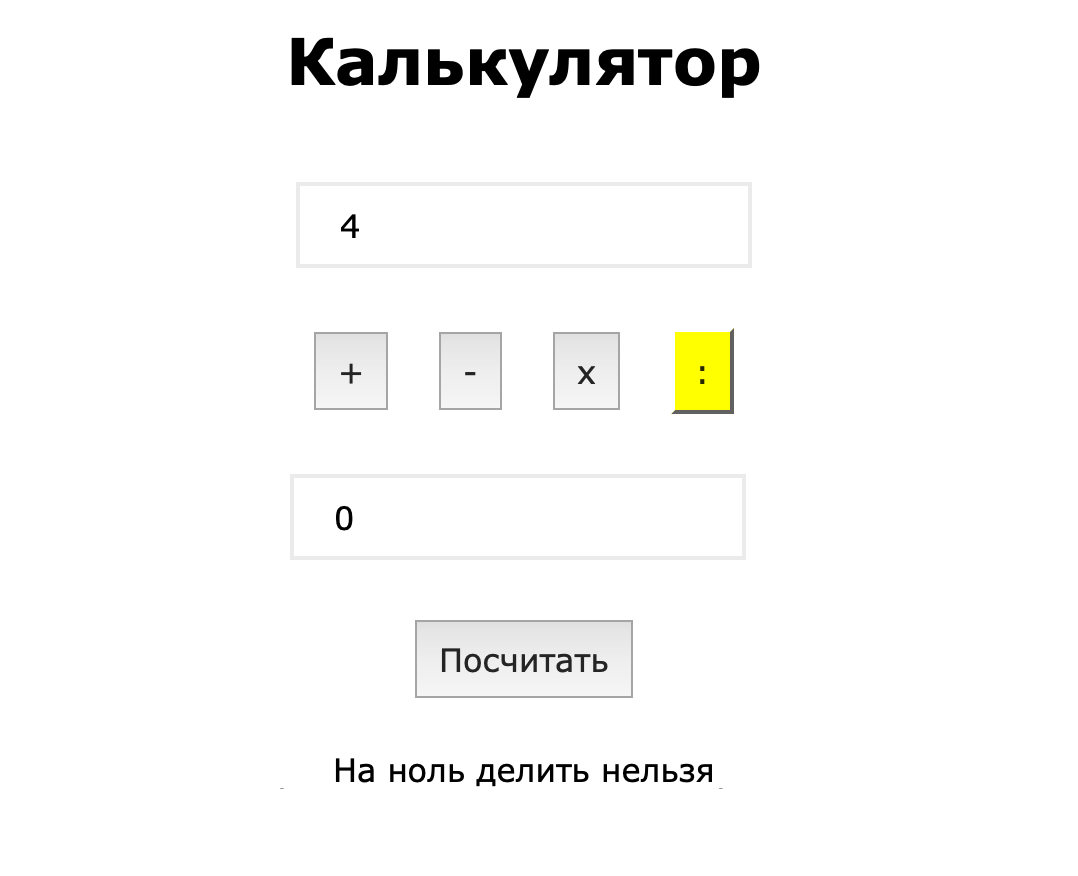
Теперь попробуем разделить на ноль:
Скрипт хитро выкрутился и записал результатом деления бесконечность. Но лучше выводить сообщение, что на ноль делить нельзя.
❌ Нет сообщения при делении на ноль.
Отказоустойчивость
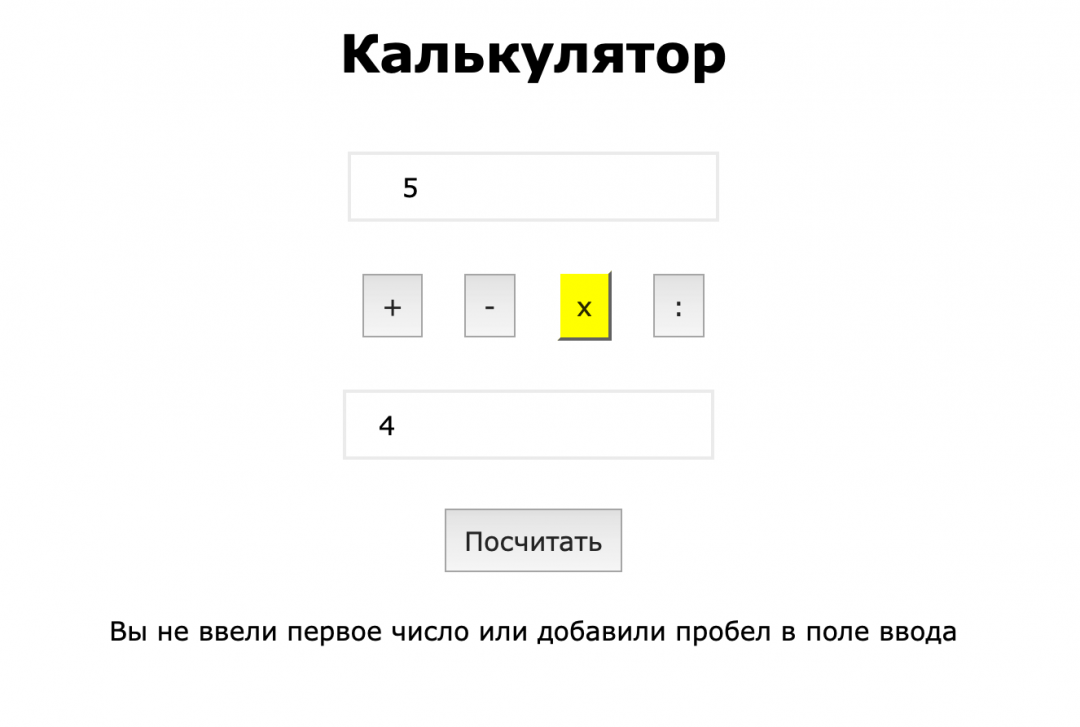
А что если оставить поле ввода пустым и попробовать что-то посчитать? Давайте посмотрим:
Скрипт преобразовал пустую строку в ноль и получил ответ, но это неправильно — при отсутствии одного из чисел калькулятор должен сообщить об этом, а не продолжать считать.
❌ Нет сообщения, если одно из чисел не введено.
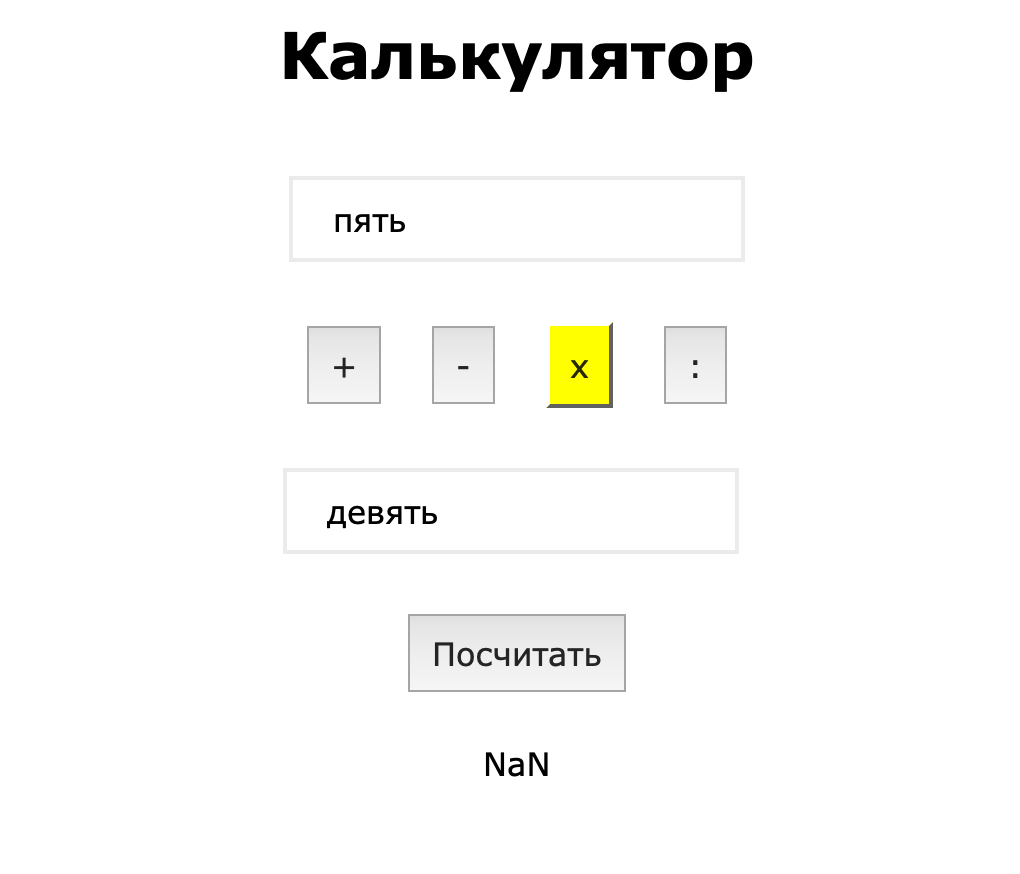
Пойдём дальше и введём слово вместо числа:
Скрипт честно пытается перевести строку в число, у него это не получается, поэтому он выдаёт неопределённое значение.
❌ Нет проверки на то, ввели число или строку.
И напоследок проверим что будет, если мы что-то введём, но не выберем ни одно действие:
Тоже плохо. Надо будет обработать такую ситуацию.
❌ Нет проверки, когда не выбрали ничего из математических действий.
Так проверяем работу калькулятора со всеми действиями, а не только с умножением. В итоге у нас получится список ошибок, которые нужно исправить.
Что делаем
После тестирования у нас получился такой список ошибок:
❌ Неправильно обрабатываются 17-значные числа и те, которые больше них.
❌ Если в ответе получается 17-значное число или более — ответ точно неверный.
❌ Нет сообщения при делении на ноль.
❌ Нет сообщения, если одно из чисел не введено.
❌ Нет проверки на то, ввели число или строку.
❌ Нет проверки, когда не выбрали ничего из математических действий.
Исправим эти ошибки. Так как все вычисления начинаются при вызове функции func(), то и править всё будем тоже внутри неё.
Проверяем, что ввели число, а не слова или другие символы
Проверяем, что нет пустых значений
JavaScript когда переводит строку в число, то пустую строку он считает как 0. Нам такой вариант не подходит, поэтому сравним её с пустой сторокой. Если она пустая — выдаём сообщение и ничего не считаем.
Ещё надо дополнительно добавить проверку на пробелы — JavaScript строку из пробелов тоже переводит как ноль, а нам это не нужно:
Обрабатываем деление на ноль
Простая проверка — добавляем сравнение второго числа с нулём:
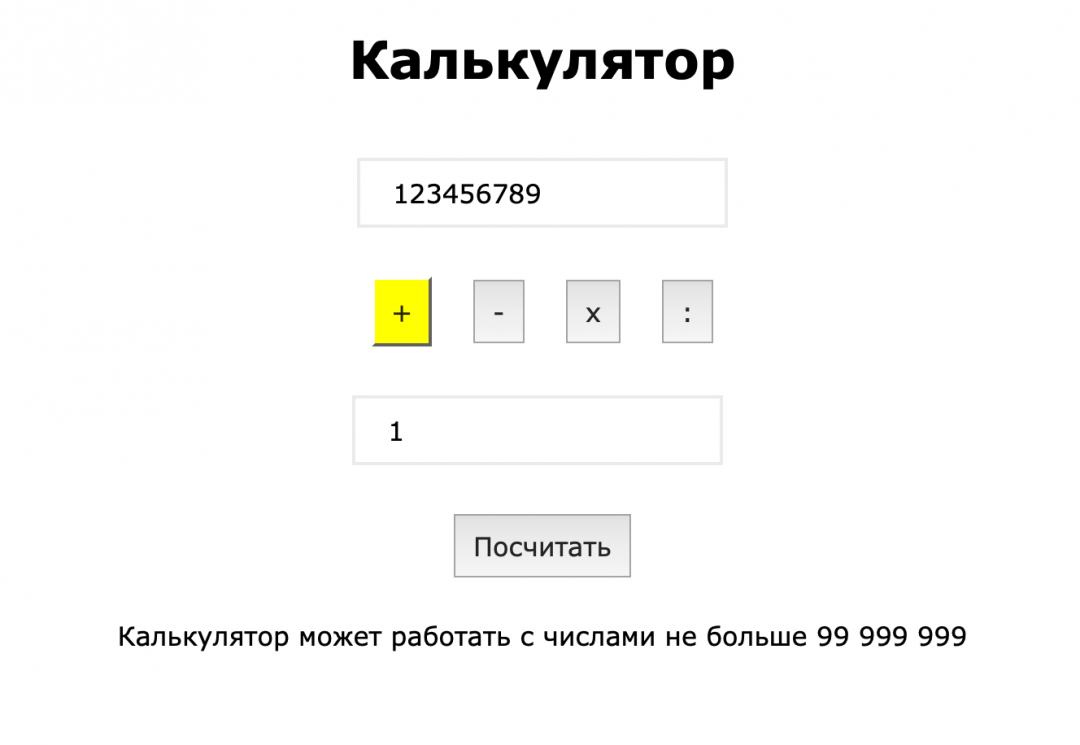
Обрабатываем длинные числа
Даже если мы ограничим каждое поле ввода числами по 16 знаков вместо 17, то при перемножении они дадут нам в ответе 32 знака — а это тоже превышает наш предел точности. Чтобы гарантированно получить в ответе число не больше 16 разрядов перед запятой, нам нужно, чтобы оба числа были не больше 99 999 999 — в нём 8 разрядов, а при перемножении мы получим максимум 16, как раз то, что нужно.
Чтобы это сделать, добавим проверку на размер числа:
Если не выбрано математическое действие
С этим всё просто — добавляем в case действие по умолчанию, которое выполнится, если никакие из вариантов не подойдут:
В итоге
✅ Калькулятор не работает с числами больше 16 знаков до запятой и предупреждает об этом пользователя
✅ В ответе всегда число, в котором не больше 16 знаков до запятой
✅ Есть проверка деления на ноль
✅ Есть сообщение, если одно из чисел не введено.
✅ Есть проверка на то, ввели число или строку.
✅ Есть проверка, когда не выбрали ничего из математических действий.
Это всё?
О нет, этот калькулятор можно гонять ещё и в хвост и в гриву:
Это (и многое другое) — и есть работа тестировщика. Круто, да?