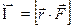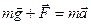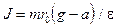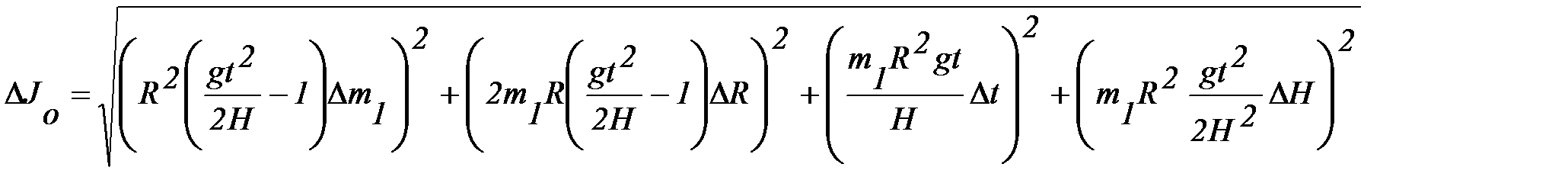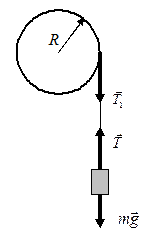на основе какого закона выводится расчетная формула для вычисления момента инерции крестовины
РАБОТА 6. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
Теоретические основы лабораторной работы
При выводе расчётных формул лабораторной работы использованы законы динамики поступательного и вращательного движения твердого тела.
Второй закон Ньютона для поступательного движения тела (m = const)
(6.1)
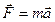
где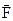 
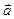
— сумма всех внешних сил, приложенных к телу; m – масса тела; 
— линейное ускорение.
Основной закон динамики вращательного движения твердого тела
(6.2)
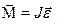
Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.
Момент инерции сплошного твёрдого тела определяется по формуле
,
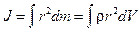
Момент силы относительно точки О это вектор, определяемый как векторное произведение радиус-вектора и силы
где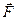 
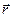
— сила, 
— радиус-вектор, проведенный из точки О, в точку приложения силы.
Момент силы относительно оси вращения это проекция вектора момента силы относительно точки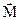 
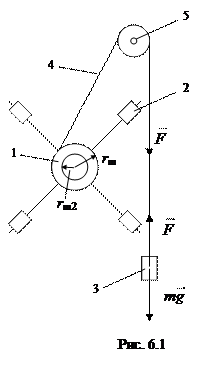
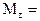
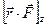
на произвольную ось z, которая проходит через точку О:
.
Основным элементом маятника Обербека (рис. 6.1) является крестовина (1), на стержнях которой размещены грузы (2). Грузы можно перемещать по стержням и закреплять в нужном положении. Крестовина с грузами насажена на вал, с двумя шкивами различных радиусов (rш). На один из шкивов наматывается нить (4), переброшенная через блок (5). К концу нити подвешен груз массой m (3). Под действием силы тяжести груза система приводится в движение.
На вертикальном штативе установлены две неподвижные рамки с оптическими осями (световые барьеры), между которыми может двигаться груз. Груз удерживается в верхнем положении электромагнитом. Время падения груза от верхнего до нижнего светового барьера фиксируется на секундомере.
На груз действует сила тяжести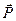 
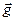
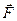
= m 
и сила натяжения 
. В соответствии со вторым законом Ньютона можно записать
В проекциях на вертикаль (с учётом знаков проекций)
(6.3)
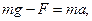
Крестовина приходит во вращательное движение под действием момента силы натяжения
Используя соотношение между угловым и линейным ускорением а e = а/r0, получим выражение для момента инерции
(6.5)
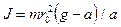
Из кинематики известно, что линейное ускорение при равноускоренном движении определяется по формуле
Таким образом, подставляя (6.6) в (6.5), получим расчётную формулу для момента инерции крестовины с грузами
(6.7)
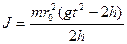
Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой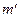 
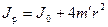
(если считать грузы материальными точками), можно выразить формулой
(6.8)
Для этого перепишем формулу (7.8) в виде
, (6.9)
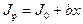
Метод наименьших квадратов позволяет найти коэффициенты уравнения (6.9) J0 и b, используя формулы
(6.10)
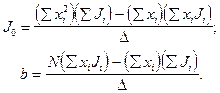
Порядок выполнения работы
1. Установить на вертикальном штативе со шкалой две неподвижные рамки (световые барьеры) на расстоянии 40-50 см друг от друга.
2. Измерить радиус шкива rш, на котором ведется эксперимент и путь, пройденный грузом.
3. Установить грузы на стержнях на максимальное расстояние от оси вращения и закрепить.
4. Включить установку нажатием кнопки «сеть».
5. Отключить электромагнит нажатием кнопки «пуск» и «сброс».
6. Выбрать необходимый груз по указанию преподавателя (табл.6.1).
| Основной груз | m = 53 г. или m = 100 г. | ||
| Перегрузы: | m1 = 1,554 г. | m6 = 2,504 г. | m10 = 19,528 г. |
| m2 = 1,705 г. | m7 = 2,714 г. | m11 = 26,258 г. | |
| m3 = 1,829 г. | m8 = 2,948 г. | m12 = 32,836 г. | |
| m4 = 2,055 г. | m9 = 12,800 г. | m13 = 39,251 г. | |
| m5 = 2,206 г. |
7. Намотать нить на шкив, установив подвешенный груз на уровне верхней рамки (над оптической осью верхнего светового барьера).
8. Закрепить груз, нажав кнопку «пуск» и обнулить счетчик (кнопка «сброс»).
9. Отпустить груз (кнопка «пуск») записать измеренное время движения груза t до оптической оси нижней рамки.
10. Произвести не менее 3-х измерений времени t и вычислить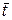 
.
11. Сместить грузы на стержнях на 1 – 2 деления к центру и повторить п.п. (3÷6), измеряя расстояние r от оси вращения до центра масс груза.
12. Повторить измерения для 8 – 10 положений грузов.
13. Записать результаты эксперимента в таблицу 6.2.
Задание 1. Определить момент инерции (Io) крестовины без грузов.
1. Освободите стержни крестовины от грузов m и убедитесь, что блок с крестовиной находится в безразличном равновесии в любом из возможных положений, когда нить с грузом m не прикреплена к блоку. Если это не так, то добейтесь состояния безразличного равновесия путем незначительного ввинчивания или вывинчивания стержней крестовины в ось блока.
2. Измерьте время движения груза m1 c высоты H. Измерения сделать 3 раза и усреднить;
3. Рассчитайте экспериментальное значение ускорения груза m1 по формуле
(1)
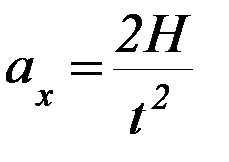
Запишем второй закон Ньютона для поступательного движения груза m1 и вращательного движения для крестовины без грузов (см. Приложение).
| x |
| m1g |
| H |
| T |
| m1 |
| ε |
| R |
где e – угловое ускорение вращения крестовины;
Т – сила натяжения нити;
R – радиус намотки нити.
Поскольку нить по блоку не скользит, то : e = а/R, тогда из системы уравнений (2) получим теоретическое значение ускорения груза m1:
(3)
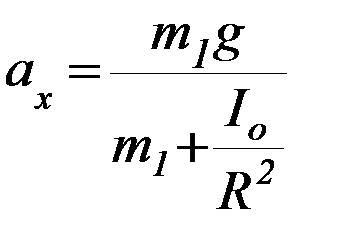
Приравняв теоретическое (3) и экспериментальное (1) выражения для ускорения груза m1, получим следующее равенство:
(4)
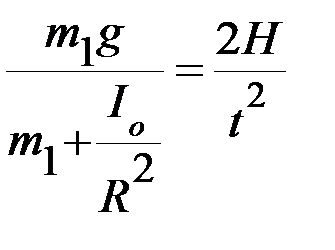
4. Из равенства (4) выразите и рассчитайте момент инерции Ioкрестовины без грузов.
Повторите пункты 2) – 4) при различных значениях H и m1. Полученные значения Ioусредните.
5. Рассчитайте погрешность определения момента инерции по формуле:
Погрешности прямым образом измеренных величин принять равными:
| ρ |
| m |
| m |
| m |
| m |
| m1 |
Задание 2. Определить момент инерции (I) крестовины с закреплёнными на ней грузами m.
1. Закрепите грузы m на указанном преподавателем расстоянии (ρ) от оси и опять проверьте, находится ли система в состоянии безразличного равновесия. Если это не так, небольшими смещениями грузов на стержнях крестовины добейтесь, чтобы это состояние имело место.
2. Установите кронштейн с верхним фотодатчиком на минимальное значение Н из рабочего интервала.
3. Закрепите один конец диска нити на диске радиуса R = r1или R = r2 по указанию преподавателя, перекиньте нить с подвешенным на другом её конце грузом (основной груз + указанное преподавателем число добавочных грузов) через неподвижный блок и добейтесь, чтобы нижний край груза m1 совпал с чертой на корпусе верхнего фотодатчика.
4. Измерьте время движения груза m1 c высоты H. Измерения сделать 3 раза и усреднить;
(5)
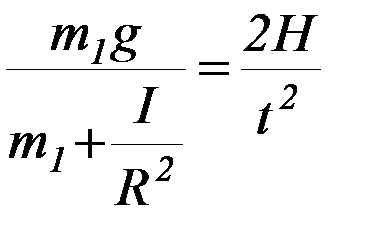
Повторите пункты 1) – 4) при разных значениях r.Полученные значения I усредните.
5. Посчитайте теоретическое значение момента инерции по формуле (6):
(6)
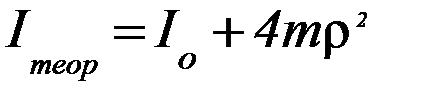
6. Оцените относительную погрешность измерений по формуле (7):
(7)
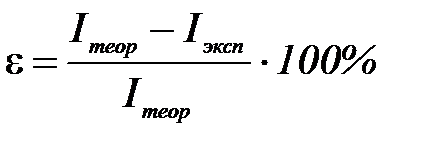
Из уравнения ( 5 ) с учетом сделанного замечания получаем окончательную формулу для расчета момента инерции крестовины
(6)
(7)
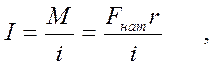
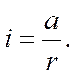
Подставляя (3) и (7) в (6), получаем окончательную формулу для расчета момента инерции крестовины
(8)
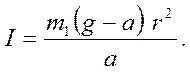
Порядок выполнения работы.
Экспериментальное определение момента инерции системы 4 х грузов.
1. Снять со стержней грузы m .
2. Намотать в один слой шнур на шкив, установив груз m1 на заранее выбранной высоте h. Отпустив крестовину, замерить время падения tо груза с помощью секундомера. Опыт повторить пять раз (при одной и той же высоте падения h ).
3. Закрепить на концах стержней грузы m.
4. Выполнить операции, указанные в пункте 2, измеряя секундомером время падения t. Опыт повторить пять раз.
5. С помощью штангенциркуля измерить диаметр шкива d в пяти разных положениях.
6. Результаты измерений занести в таблицу. Найти приближенные значения и по методу Стьюдента оценить абсолютные погрешности измерения величин tо, t и d.
7. По формуле (4) рассчитать величину линейного ускорения a, с которым падает груз m1 для случаев:
б) крестовина с грузами (а).
8. По формуле (8) вычислить момент инерции крестовины без грузов (Io) и с грузами (I), используя приближенные значения m1, R, g и полученные значения а и ао.
9. Вычислить погрешности измерений по формулам:
(9)
(10)
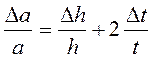
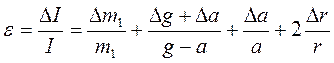
Результаты измерений и вычислений
1. Теоретически найти момент инерции системы 4 х грузов массы m, находящихся на расстоянии R от оси вращения (считая грузы материальными точками)
(11)
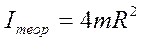
2. Сравнить результаты эксперимента и расчетов. Вычисть относительную погрешность
(12)
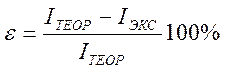
и сделать вывод о том, как велико расхождение полученных результатов.
1. Что называется моментом инерции материальной точки и произвольного тела?
2. От чего зависит момент инерции тела относительно оси вращения?
3. Приведите примеры формул момента инерции тел. Как они получены?
4. Теорема Штейнера о параллельных осях и ее практическое использование.
5. Вывод формулы для расчета момента инерции крестовины с грузами и без грузов.
Литература
4. Методические указания к выполнению лабораторных работ по разделу “Механика“.- Иваново, ИХТИ, 1989 г. (под редакцией Биргера Б.Н.).
Часть II. Колебания и волны
ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА
КОЛЕБАНИЙ МАЯТНИКА
Цель работы: определить логарифмический декремент колебаний маятника при наличии разных сил сопротивления и построить графики изменения амплитуды колебаний со временем.
Приборы и принадлежности: маятник, кювета со шкалой, приспособление для пуска маятника, секундомер, емкость с водой.
Теоретическое введение
Колебаниями называются движения или процессы, повторяющиеся во времени. Простейшим видом колебательного движения является гармоническое колебание. Оно возникает в том случае, когда на тело, выведенное из положения равновесия, действует сила F, направленная к положению равновесия и пропорциональная смещению:
где х – смещение тела от положения равновесия, k – коэффициент пропорциональности, который зависит от упругих свойств системы и называется коэффициентом квазиупругой силы. Знак минус показывает, что сила направлена противоположно смещению.
Второй закон Ньютона для материальной точки, совершающей гармоническое колебание, представляет собой дифференциальное уравнение второго порядка
, (2)
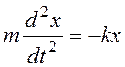
где m – масса материальной точки.
Решением уравнения (2) является выражение
где A – амплитуда колебаний, w – циклическая частота, a – начальная фаза колебаний. Аргумент периодической функции
называется фазой колебаний. При t = 0 фаза j = a. Начало отсчета можно выбрать так, чтобы a = 0, тогда
График зависимости смещения х от времени t представляет собой график гармонического колебания (рис. 1).
Чтобы распечатать файл, скачайте его (в формате Word).
Задание 1. Определить момент инерции (Io) крестовины без грузов
1. Освободите стержни крестовины от грузов m и убедитесь, что блок с крестовиной находится в безразличном равновесии в любом из возможных положений, когда нить с грузом m не прикреплена к блоку. Если это не так, то добейтесь состояния безразличного равновесия путем незначительного ввинчивания или вывинчивания стержней крестовины в ось блока.
2. Измерьте время движения груза m1 c высоты H. Измерения сделать 3 раза и усреднить;
3. Рассчитайте экспериментальное значение ускорения груза m1 по формуле
(1)
Запишем второй закон Ньютона для поступательного движения груза m1 и вращательного движения для крестовины без грузов (см. Приложение).
| x |
| m1g |
| H |
| T |
| m1 |
| ε |
| R |
где e – угловое ускорение вращения крестовины;
Т – сила натяжения нити;
R – радиус намотки нити.
Поскольку нить по блоку не скользит, то : e = а/R, тогда из системы уравнений (2) получим теоретическое значение ускорения груза m1:
(3)
Приравняв теоретическое (3) и экспериментальное (1) выражения для ускорения груза m1, получим следующее равенство:
(4)
4. Из равенства (4) выразите и рассчитайте момент инерции Ioкрестовины без грузов.
Повторите пункты 2) – 4) при различных значениях H и m1. Полученные значения Ioусредните.
5. Рассчитайте погрешность определения момента инерции по формуле:
Погрешности прямым образом измеренных величин принять равными:
| ρ |
| m |
| m |
| m |
| m |
| m1 |
Задание 2. Определить момент инерции (I) крестовины с закреплёнными на ней грузами m.
1. Закрепите грузы m на указанном преподавателем расстоянии (ρ) от оси и опять проверьте, находится ли система в состоянии безразличного равновесия. Если это не так, небольшими смещениями грузов на стержнях крестовины добейтесь, чтобы это состояние имело место.
2. Установите кронштейн с верхним фотодатчиком на минимальное значение Н из рабочего интервала.
3. Закрепите один конец диска нити на диске радиуса R = r1или R = r2 по указанию преподавателя, перекиньте нить с подвешенным на другом её конце грузом (основной груз + указанное преподавателем число добавочных грузов) через неподвижный блок и добейтесь, чтобы нижний край груза m1 совпал с чертой на корпусе верхнего фотодатчика.
4. Измерьте время движения груза m1 c высоты H. Измерения сделать 3 раза и усреднить;
(5)
Повторите пункты 1) – 4) при разных значениях r.Полученные значения I усредните.
5. Посчитайте теоретическое значение момента инерции по формуле (6):
(6)
6. Оцените относительную погрешность измерений по формуле (7):
(7)
Вывод рабочей формулы для экспериментального
определения момента инерции.
При экспериментальном определении момента инерции используется маятник Обербека, который представляет собой крестовину с четырьмя закрепленными на ней на одинаковых расстояниях от оси одинаковыми грузами. На ось крестовины насажен двухступенчатый шкив, на который намотана нить с подвешенным к ней грузом. При движении груза вниз шкив начинает вращаться. Для вывода рабочей формулы рассмотрим упрощенную схему установки, выделив систему связанных движущихся тел: поступательно движущийся груз и вращающийся шкив (рис. 4.1). Поступательное движение груза описывается уравнением:
Вращательный момент шкива создает сила натяжения нити Т1, которая по третьему закону Ньютона равна силе Т. Этот момент М = ТR. Тогда уравнение вращательного движения шкива:
Если отсутствует проскальзывание нити, то тангенциальное ускорение элементов нити, вращающихся вместе со шкивом, равно линейному ускорению груза:
Решая систему уравнений (4.1), (4.2) и (4.3), получим для момента инерции выражение: 
.
Линейное ускорение груза можно вычислить по измеренным высоте падения груза и времени его падения: h=at 2 /2.
Таким образом, получена рабочая формула для экспериментального определения момента инерции:
(4.4)
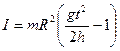
Вывод формулы для теоретического вычисления
Момента инерции.
Теоретический момент инерции после суммирования вычисляется по формуле:
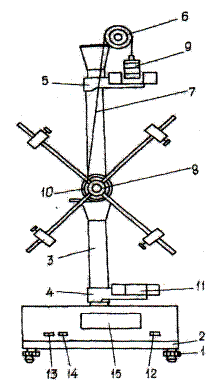
Описание экспериментальной установки
Внешний вид установки представлен на рис.4.2. Регулировочные винты 1 обеспечивают горизонтальную установку основания 2, к которому крепится вертикальная колонка 3, на которой нанесена миллиметровая шкала. К этой колонке прикреплены неподвижный кронштейн 4 и верхний подвижный 5, с помощью которого можно регулировать длину пути груза h. Через диск 6 перекинута нить 7, один конец которой прикреплен к шкиву 8, а на втором конце закреплены грузы 9. Кронштейн 11 снабжен резиновым амортизатором для ограничения движения грузов. Включение прибора производится нажатием клавиши «сеть» 12, обнуление миллисекундомера производится клавишей «сброс» 13, клавиша «пуск» 14 включает миллисекундомер. Время падения груза высвечивается на индикаторе 15.
Порядок выполнения работы
1. Включить установку в сеть.
2. Убедиться, что к нити прикреплен только один груз.
3. Намотать нить на шкив 8, а второй конец с грузом перекинуть через диск 6. Груз поднять на высоту h. Нижний край груза должен совпадать с чертой на корпусе верхнего фотодатчика.
4. Нажать кнопку «пуск» и отпустить груз без толчка. При этом запускается миллисекундомер. Записать отсчет в таблицу 4.1.
5. Нажать кнопку «сброс» и проверить, произошло ли обнуление измерителя.
6. Повторить измерение пять раз, занося значения времени падения в таблицу 4.1.
7. Последовательно увеличивая массу падающего груза, повторить п.п. 3-6.
| № измерения | Груз 1 m (г) = | Грузы 1,2 m (г) = | Грузы 1,2, 3 m (г) = | Грузы 1,2,3,4 m (г) = |
| t1 | ||||
| t2 | ||||
| t3 | ||||
| t4 | ||||
| t5 | ||||
| tср | ||||
| I |
8. Измерить высоту падения груза и длину стержня крестовины. Занести измеренные значения в таблицу 4.2. В эту же таблицу занести значения величин, указанные на установке.
| R |
| m1 |
| m2 |
| I0 |
| lc |
| l |
| h |
9. Вычислить среднее значение времени падения для каждой массы груза и занести в таблицу 4.1.
11. Рассчитать среднее значение момента инерции и оценить абсолютную и относительную погрешность его определения.
12. По формуле (4.5) вычислить теоретическое значение момента инерции маятника. Сравнить с экспериментально полученным.
13. По формуле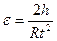 
вычислить угловое ускорение для каждого груза. Вычисленные значения занести в таблицу 4.3.
14. По формуле 
вычислить значение вращающего момента для каждой массы груза. Вычисленные значения занести в таблицу 4.3.
15. По данным таблицы 4.3 построить график зависимости углового ускорения от вращающего момента: ε = ε(М).
16. Сделать вывод, подтверждает ли характер зависимости углового ускорения от вращающего момента основной закон динамики вращательного движения. Определить возможные причины отклонения от теоретической зависимости.
17. Определить по графику среднее значение момента инерции маятника как котангенс угла наклона прямой к оси абсцисс.
18. Записать окончательные результаты работы: экспериментально полученное значение момента инерции с погрешностью, теоретическое значение момента инерции и величину момента инерции, вычисленную по графику зависимости ε = ε(М).
Контрольные вопросы
1. Дать определение момента силы относительно точки и относительно оси.
2. Дать определение момента импульса материальной точки относительно точки и относительно оси.
3. Чему равен момент импульса твердого тела относительно оси?
4. Каков физический смысл момента инерции? Как вычислить момент инерции твердого тела?
5. Провести аналогию между характеристиками поступательного и вращательного движения.
6. Указать на чертеже направление момента силы натяжения нити, действующей на шкив в данной работе.
Литература: [1, § 27, 31, 32]; [2, § 30, 33, 36]; [4, §4.1-4.3]; [5].