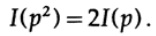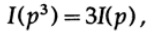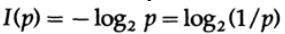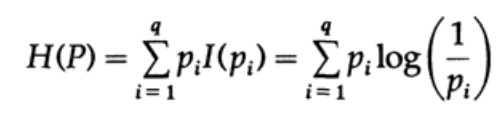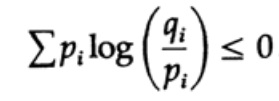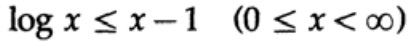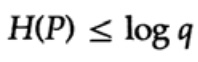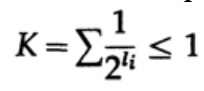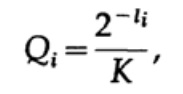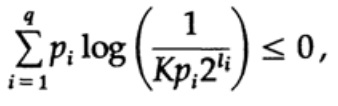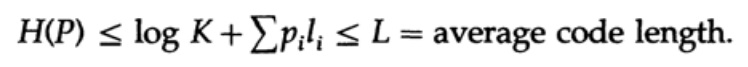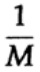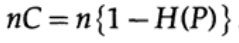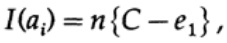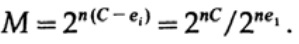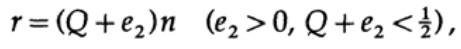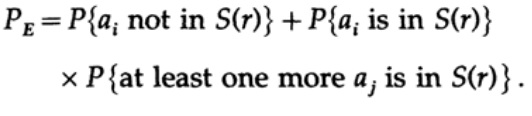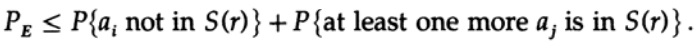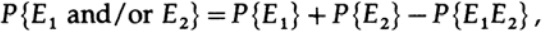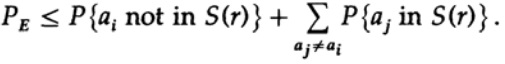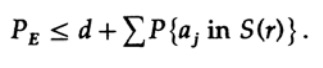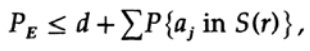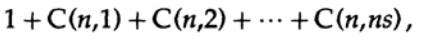теория информации и кодирования лекции
Ричард Хэмминг: Глава 13. Теория информации
«Цель этого курса — подготовить вас к вашему техническому будущему.»

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
За перевод спасибо Андрею Пахомову.
Теория Информации была разработана К. Э. Шенноном в конце 1940х годов. Руководство Лабораторий Белла настаивало, чтобы он назвал ее «Теория Связи», т.к. это намного более точное название. По очевидным причинам, название «Теория Информации» обладает значительно большим воздействием на публику, поэтому Шеннон выбрал именно его, и именно оно известно нам по сей день. Само название предполагает, что теория имеет дело с информацией, это и делает ее важной, поскольку мы все глубже проникаем в информационную эпоху. В этой главе я затрону несколько основных выводов из этой теории, приведу не строгие, а скорее интуитивно понятные доказательства некоторых отдельных положений этой теории, чтобы вы поняли, чем на самом деле является «Теория Информации», где вы можете ее применять, а где нет.
Прежде всего, что такое “информация”? Шеннон отождествляет информацию с неопределенностью. Он выбрал отрицательный логарифм вероятности события в качестве количественной меры информации, которую вы получаете при наступлении события с вероятностью p. Например, если я скажу вам, что в Лос-Анжелесе туманная погода, тогда р близок к 1, что по большому счету, не дает нам много информации. Но если я скажу, что в июне в Монтерей идет дождь, то в этом сообщении будет присутствовать неопределенность, и оно будет содержать в себе больше информации. Достоверное событие не содержит в себе никакой информации, поскольку log 1 = 0.
Остановимся на этом подробнее. Шеннон полагал, что количественная мера информации должна быть непрерывной функцией от вероятности события p, а для независимых событий она должна быть аддитивной – количество информации, полученное в результате осуществления двух независимых событий, должно равняться количеству информации, полученному в результате осуществления совместного события. Например, результат броска игральных костей и монеты обычно рассматриваются как независимые события. Переведем вышесказанное на язык математики. Если I (p) – это количество информации, которое содержится в событии с вероятностью p, то, для совместного события, состоящего из двух независимых событий x с вероятностью p1 и y с вероятностью p2 получаем

(x и y независимые события)
Это функциональное уравнение Коши, истинное для всех p1 и p2. Для решения этого функционального уравнения предположим, что
Если p1 = p 2 и p2 = p, тогда
и т.д. Расширяя этот процесс, используя стандартный метод для экспонент, для всех рациональных чисел m / n, верно следующее
Из предполагаемой непрерывности информационной меры, следует, что логарифмическая функция является единственным непрерывным решением функционального уравнения Коши.
В теории информации принято принимать основание логарифма равное 2, поэтому бинарный выбор содержит ровно 1 бит информации. Следовательно, информация измеряется по формуле
Давайте приостановимся и разберемся, что же произошло выше. Прежде всего, мы так и не дали определение понятию “информация”, мы просто определили формулу ее количественной меры.
Во-вторых, эта мера зависит от неопределенности, и, хотя она в достаточной степени подходит для машин — например, телефонных системы, радио, телевидения, компьютеров и т. д. — она не отражает нормального человеческого отношения к информации.
В-третьих, это относительная мера, она зависит от текущего состояния вашего знания. Если вы смотрите на поток “случайных чисел” из генератора случайных чисел, вы предполагаете, что каждое следующее число неопределенно, но, если вы знаете формулу для вычисления «случайных чисел», следующее число будет известно, и, соответственно, не будет содержать в себе информации.
Таким образом, определение, данное Шенноном для информации, во многих случаях подходит для машин, но, похоже, не соответствует человеческому пониманию этого слова. Именно по этой причине «Теорию информации» следовало назвать «Теорией связи». Тем не менее, уже слишком поздно чтобы менять определения (благодаря которым теория приобрела свою первоначальную популярность, и которые все еще заставляют людей думать, что эта теория имеет дело с «информацией»), поэтому мы вынуждены с ними смириться, но при этом вы должны чётко понимать, насколько определение информации, данное Шенноном, далеко от своего общеупотребительного смысла. Информация Шеннона имеет дело с чем-то совершенно другим, а именно с неопределенностью.
Вот о чем нужно подумать, когда вы предлагаете какую-либо терминологию. Насколько предложенное определение, например, определение информации данное Шенноном, согласуется с вашей первоначальной идеей и насколько оно отличается? Почти нет термина, который бы в точности отражал ваше ранее видение концепции, но в конечном итоге, именно используемая терминология отражает смысл концепции, поэтому формализация чего-то посредством чётких определений всегда вносит некоторый шум.
Рассмотрим систему, алфавит которой состоит из символов q с вероятностями pi. В этом случае среднее количество информации в системе (её ожидаемое значение) равно:
Это называется энтропией системы с распределением вероятности
Энтропия распределения вероятности играет главную роль в теории кодирования. Неравенство Гиббса для двух разных распределений вероятности pi и qi является одним из важных следствий этой теории. Итак, мы должны доказать, что
Доказательство опирается на очевидный график, рис. 13.I, который показывает, что
а равенство достигается только при x = 1. Применим неравенство к каждому слагаемому суммы из левой части:
Если алфавит системы связи состоит из q символов, то принимая вероятность передачи каждого символа qi = 1/q и подставляя q, получаем из неравенства Гиббса
Это говорит о том, что если вероятность передачи всех q символов одинакова и равна — 1 / q, то максимальная энтропия равна ln q, в противном случае выполняется неравенство.
В случае однозначно декодируемого кода, мы имеем неравенство Крафта
Теперь если мы определим псевдовероятности
где конечно 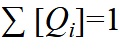
и применим немного алгебры (помните, что K ≤ 1, поэтому мы можем опустить логарифмический член, и возможно, усилить неравенство позже), то получим
где L — это средняя длина кода.
Таким образом, энтропия является минимальной границей для любого посимвольного кода со средней длиной кодового слова L. Это теорема Шеннона для канала без помех.
Теперь рассмотрим главную теорему об ограничениях систем связи, в которых информация передаётся в виде потока независимых бит и присутствует шум. Подразумевается, что вероятность корректной передачи одного бита P > 1 / 2, а вероятность того, что значение бита будет инвертировано при передачи (произойдет ошибка) равняется Q = 1 — P. Для удобства предположим, что ошибки независимы и вероятность ошибки одинакова для каждого отправленного бита — то есть в канале связи присутствует «белый шум».
Путь мы имеем длинный поток из n бит, закодированные в одно сообщение — n — мерное расширение однобитового кода. Значение n мы определим позже. Рассмотрим сообщение, состоящее из n-битов как точку в n-мерном пространстве. Поскольку у нас есть n-мерное пространство — и для простоты будем предполагать, что каждое сообщение имеет одинаковую вероятность возникновения — существует M возможных сообщений (M также будет определено позже), следовательно, вероятность любого оправленного сообщения равняется

(отправитель)
График 13.II
Далее рассмотрим идею о пропускной способности канала. Не вдаваясь в подробности, пропускная способность канала определяется как максимальный объем информации, который может быть надежно передан по каналу связи, с учётом использования максимально эффективного кодирования. Нет доводов в пользу того, что через канал связи может быть передано больше информации, чем его емкость. Это можно доказать для бинарного симметричного канала (который мы используем в нашем случае). Емкость канала, при побитовой отправки, задается как
где, как и раньше, P — вероятность отсутствия ошибки в любом отправленном бите. При отправке n независимых битов емкость канала определяется как
когда мы отправляем какое-либо из М равновероятных сообщений ai, мы имеем
При отправке n бит мы ожидаем возникновение nQ ошибок. На практике, для сообщения состоящего из n-бит, мы будем иметь приблизительно nQ ошибок в полученном сообщении. При больших n, относительная вариация ( вариация = ширина распределения, )
распределения числа ошибок будет все более узкой с ростом n.
Итак, со стороны передатчика, я беру сообщение ai для отправки и рисую сферу вокруг него радиусом
который немного больше на величину равную e2, чем ожидаемое число ошибок Q, (рисунок 13.II). Если n достаточно велико, то существует сколь угодно малая вероятность появления точки сообщения bj на стороне приемника, которая выходит за пределы этой сферы. Зарисуем ситуацию, как вижу ее я с точки зрения передатчика: мы имеем любые радиусы от переданного сообщения ai к полученному сообщению bj с вероятностью ошибки равной (или почти равной) нормальному распределению, достигающего максимума в nQ. Для любого заданного e2 существует n настолько большое, что вероятность того, что полученная точка bj, выходящая за пределы моей сферы, будет настолько малой, насколько вам будет угодно.
Теперь рассмотрим эту же ситуацию с вашей стороны (рис. 13.III). На стороне приемника есть сфера S( r) того же радиуса r вокруг принятой точки bj в n-мерном пространстве, такая, что если принятое сообщение bj находится внутри моей сферы, тогда отправленное мной сообщение ai находится внутри вашей сферы.
Как может возникнуть ошибка? Ошибка может произойти в случаях, описанных в таблице ниже:
Здесь мы видим, что, если в сфере построенной вокруг принятой точки существует еще хотя бы еще одна точка, соответствующая возможному отправленному не закодированному сообщению, то при передачи произошла ошибка, так как вы не можете определить какое именно из этих сообщений было передано. Отправленное сообщение не содержит ошибки, только если точка, соответствующая ему, находится в сфере, и не существует других точек, возможных в данном коде, которые находятся в той же сфере.
Мы имеет математическое уравнение для вероятности ошибки Ре, если было отправлено сообщение ai
Мы можем выбросить первый множитель во втором слагаемом, приняв его за 1. Таким образом получим неравенство
повторно применяем к последнему члену справа
Приняв n достаточно большим, первый член может быть принят сколь угодно малым, скажем, меньше некоторого числа d. Поэтому мы имеем
Теперь рассмотрим, как можно построить код простой замены для кодирования M сообщений, состоящих из n бит. Не имея представления о том, как именно строить код (коды с коррекцией ошибки еще не были изобретены), Шеннон выбрал случайное кодирование. Подбросьте монетку для каждого из n битов в сообщении и повторите процесс для М сообщений. Всего нужно сделать nM бросков монеты, поэтому возможны
кодовых словарей, имеющие одинаковую вероятность ½nM. Конечно, случайный процесс создания кодового словаря означает, что есть вероятность появления дубликатов, а также кодовых точек, которые будут близки друг к другу и, следовательно, будут источником вероятных ошибок. Нужно доказать, что если это не происходит с вероятностью выше, чем любой небольшой выбранный уровень ошибки, то заданное n достаточно велико.
Решающим момент заключается в том, что Шеннон усреднил все возможные кодовые книги, чтобы найти среднюю ошибку! Мы будем использовать символ Av [.], чтобы обозначить среднее значение по множеству всех возможных случайных кодовых словарей. Усреднение по константе d, конечно, дает константу, так как для усреднения каждый член совпадает с любым другим членом в сумме,
который может быть увеличен (M–1 переходит в M )
Для любого конкретного сообщения, при усреднении всех кодовых книг, кодирование пробегает все возможные значения, поэтому средняя вероятность того, что точка находится в сфере, — это отношение объема сферы к общему объему пространства. Объем сферы при этом
где s=Q+e2 Содержание книги и переведенные главы