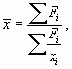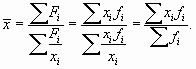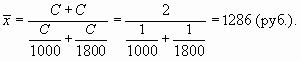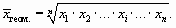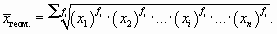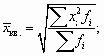для каких целей определяется среднегармоническая
Гармоническое Среднее
Что такое Гармоническое Среднее?
Гармоническое среднее – это разновидность среднего численного значения. Он рассчитывается путем деления количества наблюдений на обратную величину каждого числа в серии. Таким образом, гармоническое среднее является величиной, обратной среднему арифметическому обратных величин.
Среднее гармоническое значение 1, 4 и 4 равно:
Краткая справка
Обратное значение числа n равно 1 / n.
Основы гармонического среднего
Гармоническое среднее помогает найти мультипликативные отношения или отношения делителей между дробями, не беспокоясь об общих знаменателях. Гармонические средние часто используются для усреднения таких вещей, как скорости (например, средняя скорость движения при продолжительности нескольких поездок).
Средневзвешенное гармоническое среднее используется в финансах для усреднения мультипликаторов, таких как соотношение цены и прибыли, поскольку оно придает одинаковый вес каждой точке данных. Использование взвешенного среднего арифметического для усреднения этих соотношений даст больший вес высоким точкам данных, чем низким точкам данных, потому что соотношение цена / прибыль не нормализуется по цене, в то время как прибыль выравнивается.
Ключевые моменты
Сравнение среднего гармонического и среднего арифметического и среднего геометрического
Другие способы вычисления средних значений включают простое среднее арифметическое и среднее геометрическое. Среднее арифметическое – это сумма серии чисел, деленная на количество этой серии чисел. Если бы вас попросили найти среднее (арифметическое) среднее количество баллов за тест, вы просто сложите все баллы учащихся, а затем разделите эту сумму на количество учащихся. Например, если пять студентов сдали экзамен и их баллы составили 60%, 70%, 80%, 90% и 100%, средняя арифметическая оценка по классу будет 80%.
Среднее геометрическое среднее из набора продуктов, расчет которых обычно используется для определения результатов эффективности инвестиций или портфеля. Технически это определяется как «произведение корня n-й степени из n чисел». Среднее геометрическое должно использоваться при работе с процентами, которые выводятся из значений, в то время как стандартное среднее арифметическое работает с самими значениями.
Гармоническое среднее лучше всего использовать для таких дробей, как ставки или кратные.
Пример среднего гармонического
В качестве примера возьмем две фирмы. Один имеет рыночную капитализацию 100 миллиардов долларов и прибыль 4 миллиарда долларов (P / E 25), а другой – рыночную капитализацию 1 миллиард долларов и прибыль 4 миллиона долларов (P / E 250). В индексе, составленном из двух акций, с 10% инвестиций в первую и 90% во вторую, коэффициент P / E индекса равен:
Экспресс-подготовка к онлайн-тестированию:
для студентов дистанционного обучения, при устройстве на работу, прохождении аттестаций
Сдаешь тесты самостоятельно?
Закажи скайп-консультацию и узнай все секреты успешной сдачи экзаменов онлайн!
Статистика Тесты с ответами Тема 6-7-8
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Тема 6. Средние величины
Какими способами возможно определить среднюю арифметическую взвешенную
методом наименьших квадратов
+прямым методом: как отношение суммы произведений значений признаков на их частоты к сумме частот
Что представляет собой распределительная средняя – мода
это средняя, занимающая среднее место в ряду и делящая его на две равные части
+это средняя, характеризующая центр распределения ряда
это средняя, показывающая распространение явления в среде
это средняя, характеризующая центр изменения явления в ряду
это средняя, характеризующая изменение явления в ряду
Что представляет собой распределительная средняя – медиана
это средняя, характеризующая центр изменения явления в ряду
это средняя, характеризующая центр распределения ряда
это средняя, показывающая распространение явления в среде
+это средняя, занимающая среднее место в ряду и делящая его на две равные части
это средняя, характеризующая изменение явления в ряду
Для каких целей определяется средняя антигармоническая
когда известны значения признака и произведение значений признаков ни их частоты, а сами частоты не известны
когда определяются суммарные значения признака
+когда необходимо рассчитать распределение явления в среде
когда рассматриваются «обратные» значения признака
когда требуется получить новые значения признака
Для каких целей определяется среднегармоническая
для выявления абсолютного значения явления
для выбора середины ряда
для выявления относительной величины ряда
для расчета темпов роста явления
+для определения среднего значения ряда динамики
В каких случаях рассчитывается среднегармоническая
когда требуется получить новые значения признака
когда определяются суммарные значения признака
когда необходимо рассчитать распределение явления в среде
+когда известны значения признака и произведение значений признаков ни их частоты, а сами частоты не известны
+когда рассматриваются «обратные» значения признака
В каких случаях рассчитывается степенная средняя
когда рассчитывается сумма произведений значений признаков на их частоты
когда определяется среднее значение нелинейного вида
+когда определяется среднее значение, выраженное функцией n-ого порядка
когда определяется среднее значение линейного вида
когда рассчитывается сумма произведений значений признаков n-ого порядка на их частоты
Тема 7. Показатели и анализ вариации
Что характеризует «размах вариации»
коэффициенты вариации ряда
+это разность между максимальным и минимальным значениями признака
Размах вариации (R) – это разность между …..и … значениями признака:
однородным и взвешенным
взвешенным и наименьшим
наибольшим и средним
средним и однородным
+наибольшим и наименьшим
Как определяется дисперсия альтернативного признака
как корень квадратный из произведения вероятностей признака, положенного в основу группировки на вероятность внешнего признака
как произведение вероятностей признака, положенного в основу группировки на вероятность внешнего признака
+как произведение вероятностей наличия признака и его отсутствия
как произведение межгрупповой и средней из внутригрупповых дисперсий
как отношение межгрупповой дисперсии к средней из внутригрупповых дисперсий
Как определяется «среднеквадратическое отклонение»
как разность между максимальным и минимальным значениями признака
как средний квадрат отклонений индивидуальных значений признака от их средней величины
как среднеарифметическая из абсолютных значений отклонений отдельных вариантов от их средней
+как корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины
как средний коэффициент вариации ряда
Среднелинейное отклонение может быть:
Вариация признака изучается при помощи следующих показателей:
максимальный квадрат отклонений
+среднее линейное отклонение
произведение межгрупповой и средней из внутригрупповых дисперсий
отношение межгрупповой дисперсии к средней из внутригрупповых дисперсий
разность межгрупповой и средней из внутригрупповых дисперсий
+сумма межгрупповой и средней из внутригрупповых дисперсий
корень квадратный из произведения межгрупповой и средней из внутригрупповых дисперсий
Что характеризует межгрупповая дисперсия
случайную вариацию, полученную в результате действия случайных факторов
вариацию, полученную в результате действия внутренних факторов
вариацию, полученную в результате действия внешних факторов
вариацию, полученную в результате действия систематических и случайных факторов
+постоянную вариацию, полученную в результате действия систематических факторов
Как определяется «дисперсия»
как разность между максимальным и минимальным значениями признака
как средний коэффициент вариации ряда
+как средний квадрат отклонений индивидуальных значений признака от их средней величины
как корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины
как среднеарифметическая из абсолютных значений отклонений отдельных вариантов от их средней
С какой целью рассчитывается «корреляционное отношение»
для выявления влияния группировки на исходный результат
для расчета дисперсии
+для выявления влияния признака, положенного в основу группировки на конечный результат
для выявления влияния группировки на показатели вариации
для обоснования необходимости представленной группировки
Как определяются коэффициенты вариации ряда
как разность между любым значением ряда и средней ряда
как разность между максимальным значением ряда и средней ряда
+как отношение показателя вариации к средней ряда
+как отношение любого показателя вариации к любой средней ряда
как отношение средней к показателю вариации ряда
Что означает «правило 3-сигм»
что при нормальном распределении значение признака не входит в зону 3-сигм
что при биномиальном распределении значения признака включается в зону 3-сигм
что при распределении Пуассона распределении значения признака не включается в зону 3-сигм
что при гипергеометрическом распределении значения признака включается в зону 3-сигм
+что вариация значений признака при нормальном распределении находится в пределах трех среднеквадратических отклонений
Тема 8. Измерение связи
Какая связь между явлениями называется функциональной
связь между явлениями отсутствует
связь между явлениями чисто внешняя, то есть с внешними явлениями
связь между явлениями, в которых прослеживается статистическая закономерность в средних величинах
+связь между явлениями, в которых проявляются динамические закономерности (точная и полная)
В каких пределах изменяется индекс корреляции
в пределах от –1 до +1
в пределах от –2 до +2
+в пределах от 0 до +1
в пределах от –1 до 0
в пределах от 0 до –1
В каких пределах изменяется линейный коэффициент корреляции
в пределах от 0 до +1
в пределах от 0 до –1
+в пределах от –1 до +1
в пределах от –1 до 0
в пределах от –2 до +2
Как рассчитывается коэффициент Фехнера
как отношение разности числа пар с положительным отклонением от среднего уровня к сумме числа пар с отрицательным отклонением от среднего уровня
как отношение разности числа пар с различными знаками отклонений от средних уровней к сумме числа пар с одинаковыми различными знаками отклонений от средних уровней
как отношение суммы числа пар с отрицательным отклонением от среднего уровня к сумме числа пар с положительным отклонением от среднего уровня
как отношение разности числа пар с отрицательным отклонением от среднего уровня к сумме числа пар с положительным отклонением от среднего уровня
+как отношение разности числа пар с одинаковыми знаками отклонений от средних уровней к сумме числа пар с различными знаками отклонений от средних уровней
Какая связь между явлениями называется корреляционной
связь между явлениями чисто внешняя, то есть с внешними явлениями
связь между явлениями отсутствует
связь между явлениями, в которых проявляются динамические закономерности (точная и полная)
+связь между явлениями, в которых прослеживается статистическая закономерность в средних величинах
Средние величины в статистике
6.2. Средняя гармоническая
Средняя гармоническая величина является модифицированной формой средней арифметической. Она применяется в тех случаях, когда неизвестны значения частот у вариант ряда, зато имеются для каждого xi произведения этих вариант на соответствующие им частоты, т.д. 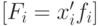
Формула средней гармонической взвешенной имеет следующий вид:
Если мы для каждой варианты рассчитаем частоту как 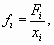
Пример 6.5. Вернемся к примеру 6.2, где рассчитывалась средняя заработная плата 20 работников малого предприятия. Предположим, что изначально были известны данные об уровне заработной платы для каждой группы работающих и начисленный им фонд заработной платы. Тогда для расчета средней заработной платы необходимо определить численность работающих в каждой группе. Для этого разделим фонд заработной платы каждой группы работающих на их уровень заработной платы (см. графу 3 в таблице). Тогда, разделив общий фонд заработной платы на общую численность работающих, получим их среднюю заработную плату.
| Исходные данные | Расчетный показатель | |
|---|---|---|
| заработная плата, руб. | фонд заработной платы, руб. | численность работающих, чел. |
| 1 | 2 | 3 |
| xi | Fi | Fi / xi |
| 5 950 | 35 760 | 6 |
| 6 790 | 54 320 | 8 |
| 7 000 | 42 000 | 6 |
| Итого | 132 080 | 20 |
Как видим, и в первом, и во втором случае расчет производился по одной и той же логической формуле
но использовались разные формулы для расчета, поскольку отличались исходные данные.
Поясним расчет. Мы знаем, что логическая формула для расчета средней цены приобретения одной акции такова:
Однако неизвестно, сколько было куплено акций каждого вида. Поэтому средняя арифметическая здесь не может быть использована.
Кроме того, мы знаем, что на покупку каждого вида акций была выделена одна и та же сумма. Обозначим ее через С. Тогда общая сумма, выделенная на покупку двух видов акций, будет равна 2С, а количество купленных акций каждого вида можно рассчитать следующим образом:
Если подставить эти значения в логическую формулу, то неизвестная величина С (сумма, выделенная на приобретение каждого вида акций) сократится, и расчет действительно будет проведен по формуле средней гармонической простой:
6.3. Средняя геометрическая
Для расчета среднего коэффициента или темпа роста статистического показателя используется формула средней геометрической.
Для несгруппированных данных (при отсутствии частот) или для сгруппированных данных с равными частотами применяется средняя геометрическая простая
Для сгруппированных данных с неравными частотами применяется средняя геометрическая взвешенная
Примеры расчета средней геометрической будут рассмотрены в гл. 9.
6.4. Средняя квадратическая и другие степенные средние
Если подставить в формулу средней степенной m = 2, то получим среднюю квадратическую:
взвешенную (для сгруппированных данных):
простую (для несгруппированных данных):
Средняя квадратическая величина широко применяется при оценке вариации признака, при изучении взаимосвязи явлений. Кроме того, прикладное значение имеет расчет степенных средних и более высоких порядков, например при изучении характеристик распределения случайных величин. Формулы для их вычисления получаются при подстановке в качестве m соответствующего показателя степени.
Правило мажорантности степенных средних состоит в том, что при расчете по одним и тем же данным между числовыми значениями средних, исчисленных по разным формулам, всегда сохраняется следующее неравенство:
Тестовые задания по статистике 84 вопроса с ответами
1. Что представляет собой «наблюдение основного массива»
а) наблюдение малозначительных величин
б) наблюдение основной единицы совокупности
в) наблюдение за совокупностью за исключением малозначительных величин-
г) наблюдение за важнейшей единицей совокупности
д) наблюдение за величинами «среднего» размера
1. Каким образом проводится «выборочное наблюдение»
а) случайным отбором нескольких единиц совокупности
б) случайным отбором нескольких единиц совокупности в необходимом количестве
+в) случайным отбором нескольких единиц совокупности в необходимом количестве при допустимой ошибке выборки-
г) заданным отбором нескольких единиц совокупности в необходимом количестве при допустимой ошибке выборки
д) заданным отбором единиц совокупности в необходимом количестве при ошибке репрезентативности
2. Какую цель преследует «монографическое наблюдение»
+а) изучение важнейшей для исследователя единицы совокупности-
б) изучение наибольшей единицы совокупности
в) изучение минимальной единицы совокупности
г) изучение минимально-возможной единицы совокупности
д) изучение минимально допустимой единицы совокупности
3. Как организуется «экспедиционный способ наблюдения»
+а) лица-регистраторы на месте проведения наблюдения сами получают необходимые сведения и заполняют формуляр наблюдений-
б) регистрируемые лица самостоятельно заполняют формуляр и отправляют его в статистические органы
в) лица-регистраторы на месте проведения наблюдения собирают заполненные регистрируемыми лицами формуляры наблюдений
г) лица-регистраторы собирают по почте заполненные регистрируемыми лицами формуляры наблюдений
д) лица-регистраторы собирают в статистических органах заполненные регистрируемыми лицами формуляры наблюдений
4. Как организуется «почтовый способ» проведения наблюдения
+а) необходимые сведения запрашиваются и передаются при помощи соответствующих органов связи-
б) необходимые сведения запрашиваются и передаются непосредственно из рук в руки
в) необходимые сведения запрашиваются и передаются через «почтовый ящик»
г) необходимые сведения по распоряжению руководящих органов собираются непосредственно лицами-регистраторами
д) необходимые сведения тайно собираются непосредственно лицами-регистраторами
5. Что представляет собой понятие «объект наблюдения»
+а) определенная совокупность единиц наблюдения, выбранная согласно поставленной цели, для исследования-
б) определенная совокупность единиц наблюдения
в) определенная генеральная совокупность
г) совокупность единиц наблюдения, имеющая наибольший удельный вес в совокупности
д) совокупность единиц наблюдения, имеющая наименьший удельный вес в генеральной совокупности
6. Что такое «критический момент» при проведении статистического наблюдения
а) срок статистического наблюдения
б) определенное число статистических единиц наблюдения
+в) определенная дата, на которую регистрируются все сведения-
г) любое число статистических единиц наблюдения
д) календарные сроки проведения наблюдения
7. Как расшифровывается понятие «место статистического наблюдения»
+а) место сбора статистических данных-
б) место обработки статистических данных
в) адрес статистического органа
г) адрес представителя статистического органа, проводящего сбор статистических данных
д) адрес местного органа власти, на территории которого проводится статистическое наблюдение
8. Какие виды «сводки статистических данных» существуют
+а) простая и сложная-
б) первичная и вторичная
в) первоначальная и производная-
г) структурная, аналитическая
д) первичная и комбинированная
9. Какие виды группировок существуют в статистических исследованиях
а) простые (структурная, аналитическая, типологическая) и сложные (комбинированные)
+б) первичные и вторичные (структурные, аналитические, типологические) и сложные (комбинированные)-
в) первоначальные и последовательные
г) удельные и структуризированные
д) исходные и последовательные
1. «Статистический график», это:
а) наглядного обобщение результатов произвольного исследования
в) изображения явления в пространстве в статике
г) изобразительная картина действительности
д) мысленное изображение закономерности
+а) словесное объяснение содержания графика и значения каждого его геометрического знака-
б) пространство размещения знаков, которое имеет определенные размеры и пропорции сторон
в) размещение знаков в поле графика
г) эталоны знака, отражающие величину геометрических знаков. Они изображаются в виде кругов, прямоугольников, квадратов и обычно выносятся с поля графика.
д) символы понятий, отражаемых на графике: точки, отрезки прямых, круги, секторы, геометрические фигуры, силуэты.
3. Масштабные ориентиры, это:
+а) эталоны знака, отражающие величину геометрических знаков. Они изображаются в виде кругов, прямоугольников, квадратов и обычно выносятся с поля графика-
в) экспликация графика
г)пространство размещения знаков
д) мысленное изображение закономерности
4.Что положено в основу деления графиков на диаграммы и статистические карты
+а) поле графика, в виде чистой бумаги, либо географической, либо контурной карты
б) экспликация графика
в) размещение знаков в поле графика
г) эталоны знака, отражающие величину геометрических знаков
5.Что отражает столбиковая диаграмма
а) многомерные показатели разных явлений
+б) единственную меру признака-
в) соотношения различных статистических совокупностей по какому-либо изменяющемуся в пространстве признаку
г) статистические совокупности по составу
д) структуру совокупности по трем признакам
6.Что выражает «Диаграммы сравнения»
+а) соотношения различных статистических совокупностей по какому-либо изменяющемуся в пространстве признаку-
б)структуру совокупности по трем признакам
в) статистические совокупности по составу
г) показывают изменения явлений во времени
д) географическое распределение отображаемого статистикой явления
7.Структурные диаграммы позволяют:
+а) сопоставить статистические совокупности по составу-
б) сопоставить статистические совокупности по времени
в) выразить явление в пространстве
г) выразить символы понятий
д) разместить знаки в поле графика
8. Диаграмма «Знаки Варзара» относится к:
+г) структурным диаграммам-
д) спиральным диаграммам
9. Динамические диаграммы:
а) позволяют сопоставить статистические совокупности по составу
б) показывают географическое распределение отображаемого статистикой явления
в) отражают явления, периодически повторяющиеся во времени
г) статистические совокупности по составу
+д) показывают изменения явлений во времени.
10. Кардиограммы позволяют:
а) составить целые статистико-географические описания
б) отражают явления, периодически повторяющиеся во времени
+в) показать географическое распределение отображаемого статистикой явления размещением на контурной географической карте специальных знаков-символов-
г) выразить явление в пространстве
д) показать структуру совокупности по трем признакам
11. Центрограммыдают возможность:
а)выразить явление в пространстве
б)показать изменения явлений во времени
+в) составить целые статистико-географические описания-
г) описать статистические совокупности по составу
д) дать соотношения различных статистических совокупностей по какому-либо изменяющемуся в пространстве признаку
1. Назначение структурной группировки
+а) определить удельный вес отдельных групп в генеральной совокупности
б) выявить влияние и взаимозависимость двух анализируемых факторов в генеральной совокупности
в) выявить возможность перегруппировки уже сгруппированных данных
г) создать новую группировку
д) выявить влияние фактора в основе группировки на результат
2. Сущность аналитической группировки
а) определить удельный вес отдельных групп в генеральной совокупности
+б) выявить влияние и взаимозависимость двух анализируемых факторов в генеральной совокупности
в) выявить возможность перегруппировки уже сгруппированных данных
г) создать новую группировку
д) выявить влияние фактора в основе группировки на результат
3.Назначение вторичной группировки
+а) перегруппировка ранее сгруппированных материалов для обеспечения сопоставимости двух или нескольких группировок
б) перегруппировка ранее сгруппированных материалов для обеспечения управляемости двумя или несколькими группировками
в) перегруппировка ранее сгруппированных материалов для создания двух или нескольких группировок
г) перегруппировка ранее сгруппированных материалов для выявления влияния факторов друг на друга
д) перегруппировка ранее сгруппированных материалов для обоснования полученных ранее выводов
4. С какой целью создаются комбинированные группировки
а) с целью учета различных признаков нескольких структурных группировок одновременно
б) с целью выявления влияния нескольких факторов на систему
+в) с целью углубленного изучения генеральной совокупности по нескольким факторам
г) с целью выявления одновременного влияния нескольких факторов на систему
д) с целью разделения генеральной совокупности по основным факторам
5. По каким направлениям проводятся вторичные группировки
а) по величине интервалов первичной группировки
+б) по удельному весу отдельных групп в общем итоге
в) по величине наибольшей группы в первичной группировке
г) по наименьшему удельному весу группы в общем итоге
д) по наибольшему удельному весу группы в общем итоге
1.Что выражают в статистике абсолютные величины
а) выражают отношение новых значений явления к принятым за базу
б) выражают количественные отношение новых значений явления к принятым за базу
+в) выражают конкретные значения исследуемого явления в натуральных единицах-
г) выражают индексы исследуемого явления
д) выражают соотношение двух сопоставимых величин в единицах или процентах
2. В чем заключается сущность относительных величин
а) они выражают отношение новых значений явления к принятым за базу
б) они выражают количественные отношение новых значений явления к принятым за базу
в) они выражают конкретные значения исследуемого явления в натуральных единицах
г) они выражают индексы исследуемого явления
+д) они выражают соотношение двух сопоставимых величин в единицах или процентах.
3. Как определяется «относительная величина структуры»
+а) как отношение заданной части совокупности ко всей совокупности-
б) как отношение заданной части совокупности к другой ее части, принятой за базу
в) как отношение одноименных показателей, относящихся к различным объектам совокупности за один и тот же период
г) как соотношение аналогичных показателей за равный период времени
д) как соотношение различных показателей, приведенных к одной базе
4. Как определяется «относительная величина координации»
а) как отношение заданной части совокупности ко всей совокупности
б) как отношение заданной части совокупности к другой ее части, принятой за базу-
в) как отношение одноименных показателей, относящихся к различным объектам совокупности за один и тот же период
г) как соотношение аналогичных показателей за равный период времени
д) как соотношение различных показателей, приведенных к одной базе
5. Как определяется «относительная величина сравнения»
а) как отношение заданной части совокупности ко всей совокупности
б) как отношение заданной части совокупности к другой ее части, принятой за базу
+г) как соотношение аналогичных показателей за равный период времени-
д) как соотношение различных показателей, приведенных к одной базе
1. Какими способами возможно определить среднюю арифметическую взвешенную
+а) прямым методом: как отношение суммы произведений значений признаков на их частоты к сумме частот
б) методом моментов
в) методом наименьших квадратов
2. В каких случаях рассчитывается среднегармоническая
+а) когда известны значения признака и произведение значений признаков ни их частоты, а сами частоты не известны-
+б) когда рассматриваются «обратные» значения признака
в) когда необходимо рассчитать распределение явления в среде
г) когда требуется получить новые значения признака
д) когда определяются суммарные значения признака
3. Для каких целей определяется средняя антигармоническая
а) когда известны значения признака и произведение значений признаков ни их частоты, а сами частоты не известны
б) когда рассматриваются «обратные» значения признака
+в) когда необходимо рассчитать распределение явления в среде
г) когда требуется получить новые значения признака
д) когда определяются суммарные значения признака
4. В каких случаях рассчитывается степенная средняя
а) когда определяется среднее значение линейного вида
б) когда рассчитывается сумма произведений значений признаков на их частоты
+в) когда определяется среднее значение, выраженное функцией n-ого порядка
г) когда рассчитывается сумма произведений значений признаков n-ого порядка на их частоты
д) когда определяется среднее значение нелинейного вида
5. Для каких целей определяется среднегармоническая
+а) для определения среднего значения ряда динамики
б) для выявления относительной величины ряда
в) для расчета темпов роста явления
г) для выявления абсолютного значения явления
д) для выбора середины ряда
6. Что представляет собой распределительная средняя – мода
+а) это средняя, характеризующая центр распределения ряда
б) это средняя, показывающая распространение явления в среде
в) это средняя, характеризующая центр изменения явления в ряду
г) это средняя, характеризующая изменение явления в ряду
д) это средняя, занимающая среднее место в ряду и делящая его на две равные части
7. Что представляет собой распределительная средняя – медиана
а) это средняя, характеризующая центр распределения ряда
б) это средняя, показывающая распространение явления в среде
в) это средняя, характеризующая центр изменения явления в ряду
г) это средняя, характеризующая изменение явления в ряду
+д) это средняя, занимающая среднее место в ряду и делящая его на две равные части
7. Что характеризует «размах вариации»
+а) это разность между максимальным и минимальным значениями признака
б) среднелинейное отклонение
г) среднеквадратическое отклонение
д) коэффициенты вариации ряда
8. Как определяется «среднелинейное отклонение»
+а) как разность между максимальным и минимальным значениями признака
б) как средний квадрат отклонений индивидуальных значений признака от их средней величины
в) как корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины
г) как средний коэффициент вариации ряда
д) как среднеарифметическая из абсолютных значений отклонений отдельных вариантов от их средней-
9. Как определяется «дисперсия»
а) как разность между максимальным и минимальным значениями признака
+б) как средний квадрат отклонений индивидуальных значений признака от их средней величины
в) как корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины
г) как средний коэффициент вариации ряда
д) как среднеарифметическая из абсолютных значений отклонений отдельных вариантов от их средней
10. Как определяется «среднеквадратическое отклонение»
а) как разность между максимальным и минимальным значениями признака
б) как средний квадрат отклонений индивидуальных значений признака от их средней величины
+в) как корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины
г) как средний коэффициент вариации ряда
д) как среднеарифметическая из абсолютных значений отклонений отдельных вариантов от их средней
11. Как определяются коэффициенты вариации ряда
+а) как отношение показателя вариации к средней ряда
+б) как отношение любого показателя вариации к любой средней ряда
в) как отношение средней к показателю вариации ряда
г) как разность между любым значением ряда и средней ряда
д) как разность между максимальным значением ряда и средней ряда
12. Какими способами возможно определить среднюю арифметическую взвешенную
+а) прямым методом: как отношение суммы произведений значений признаков на их частоты к сумме частот
+б) методом моментов-
в) методом наименьших квадратов
13. Каким способом возможно определить дисперсию
+а) прямым методом: как средний квадрат отклонений индивидуальных значений признака от их средней величины
б) методом моментов-
в) методом средних значений
г) методом первоначальных сумм
14. С какой целью рассчитывается «корреляционное отношение»
+а) для выявления влияния признака, положенного в основу группировки на конечный результат
б) для выявления влияния группировки на исходный результат
в) для выявления влияния группировки на показатели вариации
г) для обоснования необходимости представленной группировки
д) для расчета дисперсии
15. Что означает «правило 3-сигм»
+а) что вариация значений признака при нормальном распределении находится в пределах трех среднеквадратических отклонений
б) что при нормальном распределении значение признака не входит в зону 3-сигм
в) что при биномиальном распределении значения признака включается в зону 3-сигм
г) что при гипергеометрическом распределении значения признака включается в зону 3-сигм
д) что при распределении Пуассона распределении значения признака не включается в зону 3-сигм
16. Что характеризует межгрупповая дисперсия
+а) постоянную вариацию, полученную в результате действия систематических факторов
б) случайную вариацию, полученную в результате действия случайных факторов-
в) вариацию, полученную в результате действия систематических и случайных факторов
г) вариацию, полученную в результате действия внешних факторов
д) вариацию, полученную в результате действия внутренних факторов
17. Общая дисперсия, это …
+а) сумма межгрупповой и средней из внутригрупповых дисперсий
б) разность межгрупповой и средней из внутригрупповых дисперсий
в) произведение межгрупповой и средней из внутригрупповых дисперсий
г) отношение межгрупповой дисперсии к средней из внутригрупповых дисперсий
д) корень квадратный из произведения межгрупповой и средней из внутригрупповых дисперсий
18.Как определяется дисперсия альтернативного признака
а) как произведение межгрупповой и средней из внутригрупповых дисперсий
+б) как произведение вероятностей наличия признака и его отсутствия
в) как отношение межгрупповой дисперсии к средней из внутригрупповых дисперсий
г) как произведение вероятностей признака, положенного в основу группировки на вероятность внешнего признака
д) как корень квадратный из произведения вероятностей признака, положенного в основу группировки на вероятность внешнего признака
а) связь между явлениями, в которых прослеживается статистическая закономерность в средних величинах
б) связь между явлениями отсутствует
+в) связь между явлениями, в которых проявляются динамические закономерности (точная и полная)
г) связь между явлениями чисто внешняя, то есть с внешними явлениями
2. Какая связь между явлениями называется корреляционной
+а) связь между явлениями, в которых прослеживается статистическая закономерность в средних величинах
б) связь между явлениями отсутствует
в) связь между явлениями, в которых проявляются динамические закономерности (точная и полная)
г) связь между явлениями чисто внешняя, то есть с внешними явлениями
3. В каких пределах изменяется индекс корреляции
а) в пределах от –1 до +1
б) в пределах от 0 до –1
+в) в пределах от 0 до +1
г) в пределах от –1 до 0
д в пределах от –2 до +2
4. В каких пределах изменяется линейный коэффициент корреляции
+а) в пределах от –1 до +1
б) в пределах от 0 до –1
в) в пределах от 0 до +1
г) в пределах от –1 до 0
д в пределах от –2 до +2
5. Как рассчитывается коэффициент Фехнера
+а) как отношение разности числа пар с одинаковыми знаками отклонений от средних уровней к сумме числа пар с различными знаками отклонений от средних уровней
б) как отношение разности числа пар с различными знаками отклонений от средних уровней к сумме числа пар с одинаковыми различными знаками отклонений от средних уровней
в) как отношение разности числа пар с положительным отклонением от среднего уровня к сумме числа пар с отрицательным отклонением от среднего уровня
г) как отношение разности числа пар с отрицательным отклонением от среднего уровня к сумме числа пар с положительным отклонением от среднего уровня
д) как отношение суммы числа пар с отрицательным отклонением от среднего уровня к сумме числа пар с положительным отклонением от среднего уровня
1. Чем отличаются темпы прироста от темпов роста
а) темп роста равен темпу прироста
б) темп роста всегда выше темпа прироста
+в) темп прироста равен разности темпа роста минус единица (или, если в %, то минус 100%)
г) темп прироста равен сумме темпа роста плюс единица (или, если в %, то плюс 100%)
д) темп роста равен сумме темпа прироста плюс единица (или, если в %, то плюс 100%)
2. Чем различаются базисные и цепные темпы роста и прироста
3. Что характеризует среднехронологическая
а) Среднюю величину между отдельными проявлениями явления
б) Среднюю величину между частями генеральной совокупности
в) Среднюю величину между соотношениями генеральной совокупности
+г) Среднюю величину уровня явления за изучаемый период
д) Среднюю величину уровня явления в рассматриваемой совокупности
7.Что показывает коэффициент опережения среднегодовых темпов роста
+а) соотношение наибольшего к наименьшему среднегодовых темпов роста различных явлений за рассматриваемый период
б) соотношение наименьшего к наибольшему среднегодовых темпов роста различных явлений за рассматриваемый период
в) соотношение попарно наименьшего к наибольшему среднегодовых темпов роста различных явлений за рассматриваемый период
г) соотношение попарно среднегодовых темпов роста различных явлений за рассматриваемый период
д) соотношение попарно среднегодовых темпов роста каждого явления за рассматриваемый период
4. В каких случаях сглаживания рядов динамики рассчитывается «скользящая средняя»
а) в случае аналитического сглаживания
б) в случае хронологического сглаживания
+в) в случае механического сглаживания
г) в случае физического сглаживания
д) в случае корреляционного сглаживания
а) это сумма значений основного ряда динамики и значений выравненного ряда аналитическим способом
б) это разность значений основного ряда и значений выравненного ряда аналитическим способом
+в) это сумма разности значений основного ряда динамики и значений выравненного ряда аналитическим способом, взятая по модулю-
г) это сумма значений основного ряда и значений выравненного ряда аналитическим способом, взятая по модулю
д) это разность значений основного ряда и значений выравненного ряда аналитическим способом, взятая по модулю
1.Как рассчитывается сложный (агрегатный) индекс
+а) отношением суммы произведений новых значений цен и физических объемов к сумме произведений базовых значений цен и физических объемов
б) отношением суммы произведений новых значений цен и базовых физических объемов к сумме произведений базовых значений цен и базовых физических объемов
+в) отношением суммы произведений новых значений цен и новых физических объемов к сумме произведений базовых значений цен и новых физических объемов
г) отношением суммы произведений базовых значений цен и базовых физических объемов к сумме произведений базовых значений цен и новых физических объемов
д) отношением суммы произведений базовых значений цен и базовых физических объемов к сумме произведений новых значений цен и новых физических объемов
2. Как рассчитывается индекс Ласпейреса
а) отношением суммы произведений новых значений цен и физических объемов к сумме произведений базовых значений цен и физических объемов
+б) отношением суммы произведений новых значений цен и базовых физических объемов к сумме произведений базовых значений цен и базовых физических объемов
в) отношением суммы произведений новых значений цен и новых физических объемов к сумме произведений базовых значений цен и новых физических объемов
г) отношением суммы произведений базовых значений цен и базовых физических объемов к сумме произведений базовых значений цен и новых физических объемов
д) отношением суммы произведений базовых значений цен и базовых физических объемов к сумме произведений новых значений цен и новых физических объемов
3. Как рассчитывается индекс Пааше
а) отношением суммы произведений новых значений цен и физических объемов к сумме произведений базовых значений цен и физических объемов
б) отношением суммы произведений новых значений цен и базовых физических объемов к сумме произведений базовых значений цен и базовых физических объемов
+в) отношением суммы произведений новых значений цен и новых физических объемов к сумме произведений базовых значений цен и новых физических объемов
г) отношением суммы произведений базовых значений цен и базовых физических объемов к сумме произведений базовых значений цен и новых физических объемов
д) отношением суммы произведений базовых значений цен и базовых физических объемов к сумме произведений новых значений цен и новых физических объемов
4.Как определяется индекс Фишера
+а) как среднегеометрическая из индексов Ласпейреса и Пааше
б) как степенная средняя из отношения суммы произведений базовых значений цен и базовых физических объемов к сумме произведений новых значений цен и новых физических объемов
в) как среднегеометрическая из отношения суммы произведений базовых значений цен и базовых физических объемов к сумме произведений базовых значений цен и новых физических объемов
г) как среднеарифметическая из отношения суммы произведений новых значений цен и физических объемов к сумме произведений базовых значений цен и физических объемов
д) как среднегармоническая из отношения суммы произведений новых значений цен и физических объемов к сумме произведений базовых значений цен и физических объемов
5.В каких случаях рассчитывается среднеарифметический индекс
+а) когда имеются сведения только об общих объемах и индивидуальных индексах
б) когда имеется динамика явлений, уровень которой выражен средними величинами
в) когда имеется динамика индивидуальных индексов, уровень которой выражен средними величинами
г) когда имеются сведения об объемах и ценах за рассматриваемый период-
6.Как определяется индекс переменного состава
+а) как соотношение среднеарифметической, рассчитанной по новым данным к среднеарифметической, определенной по базовым значениям показателей
б) как соотношение среднегеометрической, рассчитанной по новым данным к среднегеометрической, определенной по базовым значениям показателей
в) как соотношение среднегармонической, рассчитанной по новым данным к среднегармонической, определенной по базовым значениям показателей
г) как соотношение среднехронологической, рассчитанной по новым данным к среднехронологической, определенной по базовым значениям показателей
д) как соотношение среднеарифметической, рассчитанной по новым данным к среднеарифметической, определенной по базовым значениям признака и новым значениям частоты-
7. Как определяется индекс постоянного состава
а) как соотношение среднеарифметической, рассчитанной по новым данным к среднеарифметической, определенной по базовым значениям показателей
б) как соотношение среднегеометрической, рассчитанной по новым данным к среднегеометрической, определенной по базовым значениям показателей
в) как соотношение среднегармонической, рассчитанной по новым данным к среднегармонической, определенной по базовым значениям показателей
г) как соотношение среднехронологической, рассчитанной по новым данным к среднехронологической, определенной по базовым значениям показателей
+д) как соотношение среднеарифметической, рассчитанной по новым данным к среднеарифметической, определенной по базовым значениям признака и новым значениям частоты
8. Как определяется индекс структуры
+а) как соотношение среднеарифметической, рассчитанной по базовым значениям признака и новым значениям частоты к среднеарифметической, определенной по базовым значениям признака и базовым значениям частоты
б) как соотношение среднеарифметической, рассчитанной по новым значениям признака и новым значениям частоты к среднеарифметической, определенной по базовым значениям признака и базовым значениям частоты
в) как соотношение среднеарифметической, рассчитанной по новым значениям признака и базовым значениям частоты к среднеарифметической, определенной по базовым значениям признака и базовым значениям частоты
г) как соотношение среднегармонической, рассчитанной по новым значениям признака и базовым значениям частоты к среднегармонической, определенной по базовым значениям признака и базовым значениям частоты
д) как соотношение среднеантигармонической, рассчитанной по новым значениям признака и базовым значениям частоты к среднеантигармонической, определенной по базовым значениям признака и базовым значениям частоты
1.В каких случаях производится малая выборка
а) когда объем генеральной совокупности не превышает 100 единиц
б) в случае отсутствия данных о численности генеральной совокупности
+в) когда объем генеральной совокупности не превышает 30 единиц
г) в случае отсутствия данных о составе генеральной совокупности
д) когда объем генеральной совокупности не превышает 10 единиц
2 Что характеризует коэффициент Пирсона
а) отношение разности эмпирических и теоретических частот к сумме теоретических частот
+б) отношение суммы разностей эмпирических и теоретических частот к сумме теоретических частот
в) соотношение эмпирических частот к сумме теоретических частот
г) сумма эмпирических и теоретических частот
д) разность эмпирических и теоретических частот
3. Как устанавливается значение t при проведении выборочного наблюдения
а) на основе случайных величин в пределах от 1 до 10
+б) самостоятельно исходя из правила «3-сигм», устанавливая заданную предельную ошибку
в) самостоятельно исходя из генеральной средней и доли
г) на основе предельной ошибки средней и доли
д) на основе дисперсии
4. Каким образом полученные при выборке данные могут быть перенесены на всю генеральную совокупность
+а) через поправочный коэффициент
б) через корреляцию полученных данных
в) прямым пересчетом: умножением полученных данных на объем генеральной совокупности-
г) путем дисперсионного пересчета
д) через соотношение среднеарифметической выборочной и генеральной